本文继续介绍重要的贪心算法,比如哈夫曼编码、最小生成树等算法。
最优前缀码及哈夫曼编码
二元前缀码
二元前缀码:用0-1字符串作为代码表示字符,要求任何字符的代码都不能作为其它字符代码的前缀。
非前缀码的例子:
a: 001, b: 00, c: 010, d: 01
解码的歧义,例如字符串0100001
-
解码1:01,00,001 ⟹ d,b,a
-
解码2:010,00,01 ⟹ c,b,d
前缀码的二叉树表示
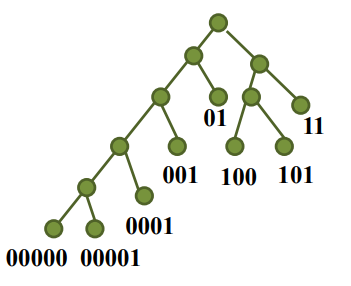
前缀码:{00000,00001,0001,001,01,100,101,11}
构造树:
-
0 —— 左子树
-
1 —— 右子树
-
码对应着一片树叶
-
最大位数为数深
平均传输位数计算公式:B=i=1∑nf(xi)d(xi)
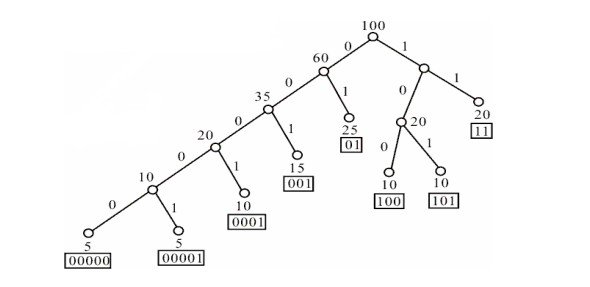
计算得到:B=[(5+5)×5+10×4+(15+10+10)×3+(25+20)×2]/100=2.85
*问题:*给定字符集C={x1,x2,...,xn}和每个字符的频率f(xi),i=1,2,...,n。求关于C的一个最有前缀码(平均传输位数最小)。
哈夫曼算法
伪代码
算法 Huffman©
输入:C={x1,x2,...,xn)},f(xi)=1,2,...,n。
输出:Q // 队列
-
n←∣C∣
-
Q←C // 频率递增队列Q
-
fori←1ton−1do
-
z← Allocate-Node() // 生成节点z
-
z.left()←Q中的最小元 // 最小作z左儿子
-
z.right←Q中的最小元 // 最小作z右儿子
-
f(z)←f(x)+f(y)
-
Insert(Q,z) // 将z插入Q
-
returnQ
Python实现哈夫曼树
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| from typing import Optional, Tuple, Any, List
class Node:
_name: str
_value: int
_left: Any
_right: Any
def __init__(self, name: Optional[str], value: Optional[str]):
self._name = name
self._value = value
self._left = Optional[Node]
self._right = Optional[Node]
class HuffmanTree(object):
Node_Queue: List[Node]
huffman_code: List[int]
root: Node
def __init__(self, char_weights: Tuple[str, int]):
self.Node_Queue = [Node(weight[0], weight[1]) for weight in char_weights]
while len(self.Node_Queue) != 1:
self.Node_Queue.sort(key=lambda node: node._value, reverse=True)
tmp = Node(name=None, value=(self.Node_Queue[-1]._value+self.Node_Queue[-2]._value))
tmp._left = self.Node_Queue.pop(-1)
tmp._right = self.Node_Queue.pop(-1)
self.Node_Queue.append(tmp)
self.root = self.Node_Queue[0]
self.huffman_code = [0 for i in range(10)]
def pre(self, tree: Node, length: int):
node = tree
if not node:
return
elif node._name:
print(node._name + '的编码为' + ''.join([str(i) for i in self.huffman_code[0:length]]))
return
self.huffman_code[length] = 0
self.pre(node._left, length + 1)
self.huffman_code[length] = 1
self.pre(node._right, length + 1)
def get_code(self):
self.pre(self.root, 0)
if __name__ == '__main__':
char_weights = [('a', 5), ('b', 4), ('c', 10), ('d', 8), ('f', 15), ('g',2)]
tree = HuffmanTree(char_weights)
tree.get_code()
|
实例
输入:a:45;b13;c:12;d:16;e:9;f:5
能够得到下面的二叉树:
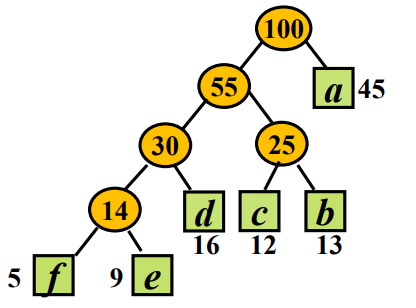
编码为:
-
f 0000
-
e 0001
-
d 001
-
c 010
-
b 011
-
a 1
平均传输位数:2.24
最优前缀码性质
引理1:C是字符集,∀c∈C,f(c)为频率,x,y∈C,f(x),f(y)频率最小,那么存在最优二元前缀码使得x,y码字等长且仅在最有一位不同。
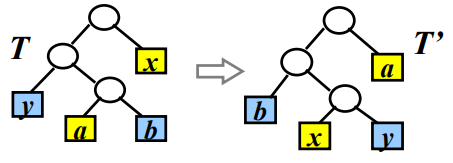
B(T)−B(T′)=i∈C∑f[i]dT(i)−i∈C∑f[i]dT′(i)≥0,其中dT(i)为i在T中的层数(i到根的距离)。
引理2:设T是二元前缀码的二叉树,∀x,y∈T,x,y是树叶兄弟,z是x,y的父亲,令T′=T−x,y,且令z的频率f(z)=f(x)+f(y)。T′是对应二元前缀码C′=(C−{x,y})∪{z}的二叉树,那么B(T)=B(T′)+f(x)+f(y)。
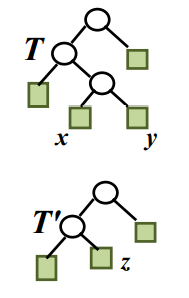
引理2证明:
证 ∀c∈C−{x,y},有
dT(c)=dT,(c)⟹f(c)dT(c)=f(c)dT,(c)dT(x)=dT(y)=dT,(z)+1
B(T)=i∈T∑f(i)dT(i)=i∈T,i=x,y∑f(i)dT(i)+f(x)dT(x)+f(y)dT(y)=i∈T′,i=z∑f(i)dT′(i)+f(z)dT′(z)+(f(x)+f(y))=B(T′)+f(x)+f(y)
哈夫曼编码的正确性证明
算法正确性证明思路
定理:Huffman算法对任意规模为n(n≥2)的字符集C都得到关于C的最优前缀码的二叉树。
归纳基础 证明:对于n=2的字符集,Huffman算法得到最优前缀码。
归纳步骤 证明:假设Huffman算法对于规模为k的字符集都得到最优前缀码,那么对于规模为k+1的字符集也得到最有前缀码。
归纳基础
n=2,字符集C={x1,x2}
对任何代码的字符至少都需要1位二进制数字。Huffman算法得到的代码是0和1,是最优前缀码。
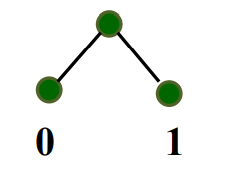
归纳步骤
假设Huffman算法对于规模为k的字符集都得到最有前缀码。考虑规模为k+1的字符集
C={x1,x2,...,xk+1},
其中x1,x2∈C是频率最小的两个字符。
令 C′=(C−{x1,x2})∪{z},f(z)=f(x1)+f(x2)
根据归纳假设,算法得到一颗关于字符集C′,频率f(z)和f(xi)(i=3,4,...,k+1)的最有前缀码的二叉树T′。
把x1,x2作为z的儿子附到T′上,得到树T,那么T是关于C=(C′−{z}∪{x1,x2})的最有前缀码的二叉树。
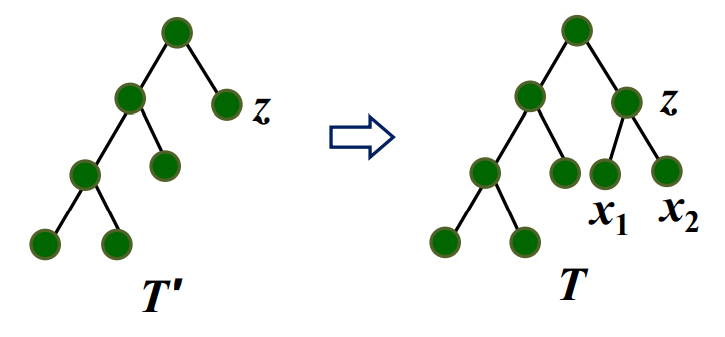
如果不然,则存在更优树T∗,B(T∗)<B(T),且由引理1,其树叶兄弟是x1和x2。
去掉T∗中x1和x2,得到T∗′。根据引理2,
B(T∗′)=B(T∗)−(f(x1)+f(x2))<B(T)−(f(x1)+f(x2))=B(T′)
与T′是一颗关于C′的最有前缀码的二叉树矛盾。
应用:文件归并
问题:给定一组不同长度的排好序文件构成的集合S={f1,...,fn},其中fi表示第i个文件含有的项数。使用二分归并将这些文件归并成一个有序文件。
归并过程对应于二叉树:文件为树叶,fi与fj归并的文件是它们的父节点。
两两顺序归并
实例:S={21,10,32,41,18,70}
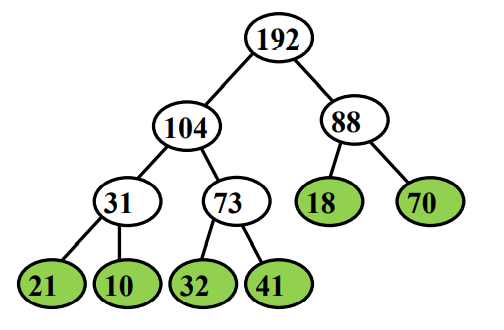
(1) (21+10−1)+(32+41−1)+(18+70−1)+(31+73−1)+(104+88−1)=483
(2) (21+10+32+41)×3+(18+70)×2−5=483
代价计算公式:i∈S∑d(i)fi−(n−1)
实例:Huffman树归并
输入:S={21,10,32,41,18,70}
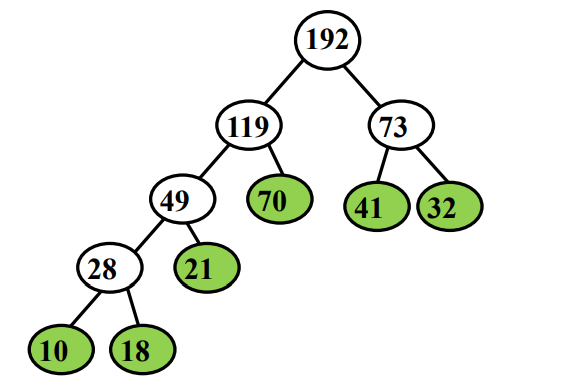
代价:(10+18)×4+21×3+(70+41+32)×2−5=456
最小生成树
Prim算法
Kruskal算法
单源最短路径问题及算法
Dijkstra算法的证明








