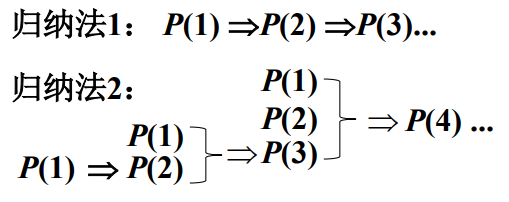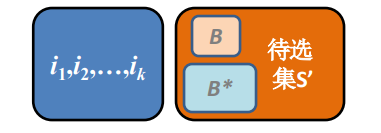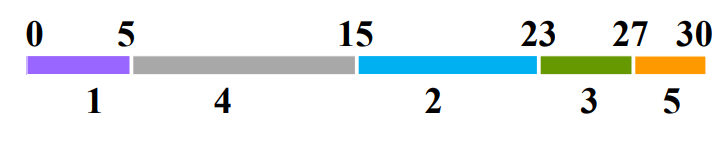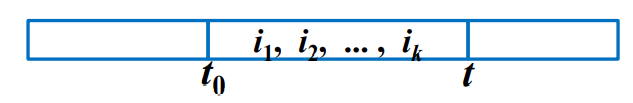贪心算法基础

本文开始记录贪心算法的学习。

贪心算法的例子——活动选择问题

输入：$S=\{1,2,...,n\}$为$n$项活动的集合，$s_i$、$f_i$分别为活动$i$的开始和结束时间。

活动$i$ 与$j$相容 $\iff s_i \ge f_j$ 或 $s_j \ge f_i$

求：最大的两两相容的活动集$A$

输入实例：

$i$	1	2	3	4	5	6	7	8	9	10
$s_i$	1	3	2	5	4	5	6	8	8	2
$f_i$	4	5	6	7	9	9	10	11	12	13

解：$\{1,4,8\}$

贪心算法

贪心算法（greedy algorithm）的挑选过程是多步判断，每步依据某种“短视”的策略进行选择，选择时注意满足条件相容性条件。

策略1：开始时间早的优先排序使$s_1\le s_2 \le ... \le s_n$，从前向后挑选；

策略2：占用时间少的优先排序使得$f_1-s_1 \le f_2 - s_2 \le ... \le f_n - s_n$，从前向后挑选。

策略3：结束早的优先排序使得$f_1 \le f_2 \le ... \le f_n$，从前向后挑选。

策略1的反例

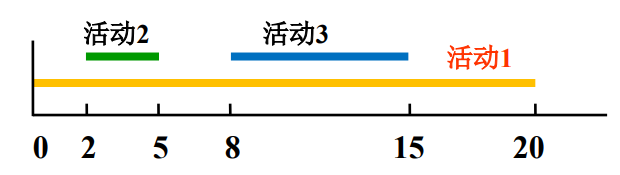
策略1：开始早的优先

反例：$S=\{1,2,3\}$

$s_1=0,f_1=20,s_2=2,f_2=5,s_3=8,f_3=15$

策略2的反例

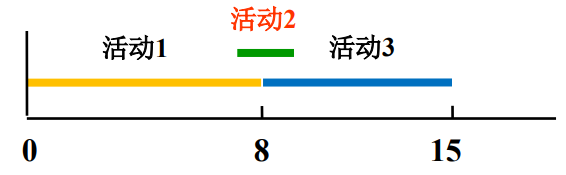
策略2：占时少的优先

反例：$S=\{1,2,3\}$

$s_1=0,f_1=8,s_2=7,f_2=9,s_3=8,f_3=15$

策略3伪码

算法：Greedy Select

输入：活动集$S, s_i, f_i, i=1,2,...,n, f_1 \le ... \le f_n$

输出：$A \subseteq S$，选中的活动子集

1. $n \gets length[S]$

2. $A \gets \{1\}$

3. $j \gets 1$

4. for $i \gets 2$ to $n$ do

5. $\quad \quad if \quad s_i \ge f_j$

6. $\quad \quad then \quad A \gets A \cup \{i\}$

7. $\quad \quad \quad \quad \quad j \gets i$

8. return A

完成事件 $t=\max \{f_k: k \in A\}$

运行实例

输入：$S=\{1,2,...,10\}$

$i$	1	2	3	4	5	6	7	8	9	10
$s_i$	$\fcolorbox{red}{aqua}{1}$	3	0	$\fcolorbox{red}{aqua}{5}$	3	5	6	$\fcolorbox{red}{aqua}{8}$	8	2
$f_i$	$\fcolorbox{red}{aqua}{4}$	5	6	$\fcolorbox{red}{aqua}{7}$	8	9	10	$\fcolorbox{red}{aqua}{11}$	12	13

解：$A=\{1,4,8\},\quad t=11$

时间复杂度：$O(n \log n) + O(n)=O(n\log n)$

贪心算法的特点

设计要素：

1. 贪心算法适用于组合优化问题；

2. 求解过程是多步判断过程，最终的判断序列对应于问题的最优解；

3. 依据某种“短视”的贪心选择性质判断，性质好坏决定算法的成败；

4. 贪心法必须进行正确性证明；

5. 证明贪心法不正确的技巧：举反例。

贪心算法的正确性证明

一个数学归纳法的例子

例：证明对于任何自然数$n$，$1+2+...+n=n(n+1)/2$

证 $n=1$，左边$=1$，右边$=1 \times (1+1)/2=1$

假设对任意自然数$n$等式成立，则

$\large 1+2+...+(n+1) \\ =(1+2+...+n)+(n+1) \\ =n(n+1)/2 + (n+1) \\ =(n+1)(n/2+1) \\ =(n+1)(n+2)/2$

第一数学归纳法

适合证明涉及自然数的命题$P(n)$

归纳基础：证明$P(1)$为真（或者$P(0)$为真）

归纳步骤：若对所有$n$有$P(n)$为真，证明$P(n+1)$为真

$\forall n, P(n) \to P(n+1) \\ \quad \quad \quad P(1) \\ n=1,\quad P(1) \implies P(2) \\ n=2,\quad P(2) \implies P(3) \\ \quad \quad \quad ...$

第二数学归纳法

适合证明涉及自然数的命题$P(n)$

归纳基础：证明$P(1)$为真（或$P(0)$为真）

归纳步骤：若对所有小于$n$的$k$有$P(k)$真，证明$P(n)$为真

$\forall k(k<n \land P(k)) \to P(n) \\ \quad \quad \quad P(1) \\ n=2, P(1) \implies P(2) \\ n=3, P(1) \land P(2) \implies P(3) \\ \quad \quad \quad ...$

两种归纳法的区别

归纳基础一样：$P(1)$为真

归纳步骤不同：

证明逻辑

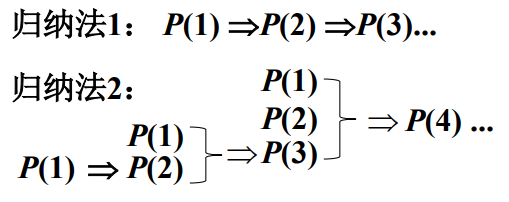
算法正确性归纳证明

证明步骤：

1. 叙述一个有关自然数$n$的命题，该命题断定该贪心策略的执行最终将导致最优解。其中自然数$n$可以代表算法步数或问题规模。

2. 证明命题对所有的自然数为真。

   归纳基础（从最小实例规模开始）

   归纳步骤（第一或第二数学归纳法）

活动选择算法的命题

命题：

算法Select执行到第$k$步，选择$k$项活动

$\quad \quad i_1=1,i_2,...,i_k$

则存在最优解$A$包含活动$i_1=1,i_2,...,i_k$。

根据上述命题：对于任何$k$，算法前$k$步的选择都将导致最优解，至多到第$n$步将得到问题实例的最优解。

归纳证明：归纳基础

令$S=\{1,2,...,n\}$是活动集，且$f_i\le ...\le f_n$。

归纳基础：$k=1$，证明存在最优解包含活动$1$

证： 任取最优解A，A中的活动按截止时间递增排列。如果$A$的第一个活动为$j,j \not 1$，用$1$替换$A$的活动j得到解$A'$，即

$\quad \quad \quad A' = (A-\{j\}) \cup \{1\}$，

由于$f_1 \le f_j$，$A'$也是最优解，且含有1。

归纳步骤

假设命题对$k$为真，证明对$k+1$也为真

证明：算法执行到第k步，选择了活动$i_1=1,i_2,...,i_k$，根据归纳假设存在最优解A包含$i_1=1,i_2,...,i_k$，$A$中剩下活动选自集合$S'$

$S'=\{i|i \in S, s_i \ge f_k\} \\ A=\{i_1,i_2,...,i_k\} \cup B$

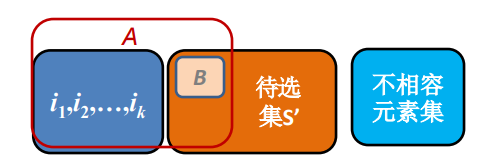
$B$是$S'$的最优解。（若不然，$S'$的最优解为$B^*$，$B^*$的活动比B多，那么

$\quad \quad \quad B^* \cup \{1,i_2,...,i_k\}$

是$S$的最优解，且比$A$的活动多，与$A$的最优性矛盾。）

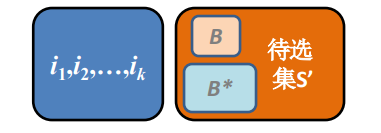
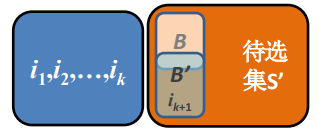
将$S'$看成子问题，根据归纳基础，

存在$S'$的最优解$B'$有$S'$中的第一个活动$i_{k+1}$，且$|B'|=|B|$，于是

$\{i_1,i_2,...,i_k\} \cup B' \\ =\{i_1,i_2,...,i_k,i_{k+1}\} \cup (B'-\{i_{k+1}\})$

也是原问题的最优解。

最优装载问题

问题：$n$个集装箱$1,2,...,n$装上轮船，集装箱$i$的重量$w_i$，轮船装载限制为$C$，无体积限制。问如何装使得上船的集装箱最多？不妨设每个箱子的重量$w_i\le C$。

算法设计

• 贪心策略：轻者优先

• 算法设计：

  将集装箱排序，使得

  $w_1 \le w_2 \le ... \le w_n$

  按照标号从小到大装箱，直到装入下一个箱子使得集装箱总重量超过轮船装载重量限制，则停止。

正确性证明思路

• 命题：对装载问题任何规模为$n$的输入实例，算法得到最优解。

• 设集装箱从轻到重记为$1,2,...,n$。

  归纳基础 证明对任何只含1个箱子的输入实例，贪心法得到最优解，显示正确。

• 归纳步骤 证明：假设对于任何n个箱子的输入实例贪心法都能得到最优解，那么对于$n+1$个箱子的输入实例也能得到最优解。

归纳步骤证明思路

$N=\{1,2,...,n+1\},w_1\le w_2 \le ... \le w_{n+1}$

$\implies$

去掉箱子$1$，令$C'=C-w_1$，得到规模为$n$的输入$N'=\{2,3,...,n+1\}$

$\implies$

关于输入$N'$和$C'$的最优解$I'$

$\implies$

在$I'$加入箱子$1$，得到$I$

$\implies$

证明$I$是关于输入$N$的最优解

正确性证明

假设对于$n$个集装箱的输入，贪心法都可以得到最优解，考虑输入

$N=\{1,2,...,n+1\}$，其中$w_1\le w_2 \le ... \le w_{n+1}$

由归纳假设，对于

$N'=\{2,3,...,n+1\}, \quad C'=C-w_1$，

贪心法得到最优解$I'$。令

$I=I'\cup \{1\}$

---

$I$(算法解)是关于$N$的最优解。

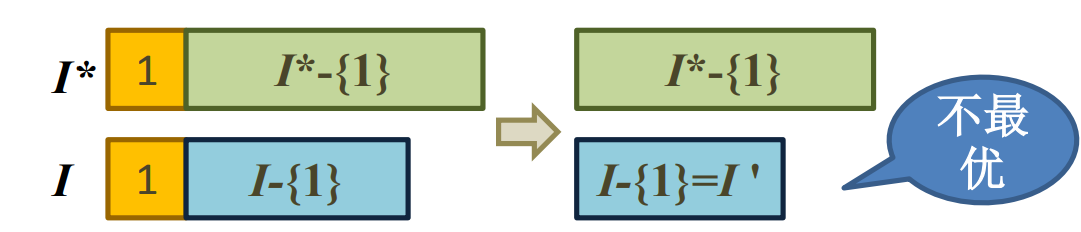
若不然，存在包含1的关于N的最优解$I*$（如果$I*$）
若不然，存在包含1的关于N的最优解$I*$（如果$I*$中没有1，用1替换中的第一个元素得到的解也是最优解），且$|I*|>|I|$；那么$I*-\{1\}$是$N'$和$C'$的解且

$|I*-\{1\}|>|I-\{1\}|=|I'|$

与$I'$是关于$N'$和$C'$的最优解矛盾。

小结

• 装载问题是0-1背包的子问题（每件物品的重量为1），NP难的问题存在多项式时间可解的子问题。

• 贪心算法证明：对规模归纳

最小延迟调度

客户集合$A$，$\forall i \in A$，$t_i$为服务时间，$d_i$为客户要求完成时间，$t_i, d_i$为正整数，一个调度$f:A\to N$，$f(i)$为客户$i$的开始时间。求最大延迟达到最小的调度，即求$f$使得

$\min_f\{\max_{i \in A}\{f(i)+t_i-d_i\}\} \\ \forall i,j \in A, i \neq j,f(i)+t_i \le f(j) \\ or \quad f(j)+t_j\le f(i)$

实例：调度1

$A=\{1,2,3,4,5\},T=\{5,8,4,10,3\},D=<10,12,15,11,20>$。

调度1：顺序安排

$f_1(1)=0,f_1(2)=5,f_1(3)=13,f_1(4)=17,f_1(5)=27$

各任务延迟：0，1，2，16，10；

最大延迟：16。

优化的调度2

$A=\{1,2,3,4,5\},T=\{5,8,4,10,3\},D=<10,12,15,11,20>$。

调度2：按截至时间从前到后安排：

$f_2(1)=0,f_2(2)=5,f_2(3)=13,f_2(4)=17,f_2(5)=27$

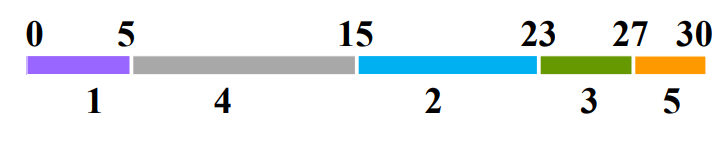
各个任务延迟：0，11，12，4，10；

最大延迟：12。

贪心策略

贪心策略1：按照$t_i$从小到大安排

贪心策略2：按照$d_i-t_i$从小到大安排

贪心策略3：按照$d_i$从小到大安排

策略1对某些实例得不到最优解。

• 反例：$t_1=1,d_1=100,t_2=10,d_2=10$

策略2对某些实例得不到最优解。

• 反例：$t_1=1,d_1=2,t_2=10,d_2=10$

策略3

伪代码

算法 Schedule

输入：A，T，D

输出：f

1. 排序A使得$d_1\le d_2 \le ... \le d_n$

2. $f(1)\gets 0$ // 从0时刻起

3. $i \gets 2$

4. $while \quad i \le n \quad do$

5. $\quad \quad \quad f(i) \gets f(i-1)+t_{i-1}$

6. $\quad \quad \quad i\gets i+1$

---

排序思想：按照完成时间从早到晚安排任务，没有空闲。

交换论证：正确性证明

证明思路：

• 分析一般最优解与算法解的区别（成分，排列顺序不同）；

• 设计一种转换操作（替换成份或者交换次序），可以在有限步将任意一个普通最优解逐步替换成算法的解；

• 上述每部转换都不降低解的最优性质。

贪心算法的解的性质：没有空闲时间，没有逆序

逆序$(i,j): f(i)<f(j)且d_i>d_j$

引理

引理1：所有没有逆序、没有空闲时间的调度具有相同的最大延迟。

证：设$f$没有逆序，在$f$中具有相同的完成时间$d$的客户$i_1,i_2,...,i_k$连续安排，其安排时刻为$t_0$，完成这些任务的时刻是$t$，最大延迟为最后任务延迟$t-d$，与$i_1,i_2,...,i_k$的排列次序无关。

$t=t_0+(t_{i_1}+t_{i_2})+...+t_{i_{k}}$

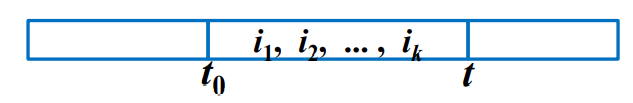
证明要点

从一个没有空闲的最优解出发，逐步转变成没有逆序的解。根据引理1，这个解和算法解具有相同的最大延迟。

1. 如果一个最优调度存在逆序，那么存在$i<n$使得$(i,i+1)$构成一个逆序，称为相邻的逆序。

2. 交换相邻逆序$i$和$j$，得到的解仍旧最优。

3. 每次交换后逆序数减$1$，至多经过$n(n-1)/2$次交换得到一个没有逆序的最优调度——等价于算法的解。

交换相邻逆序仍旧最优

设$f_1$是一个任意最优解，存在相邻逆序$(i,j)$。交换$i$和$j$的顺序，得到解$f_2$。那么$f_2$的最大延迟不超过$f_1$的最大延迟。

理由：

1. 交换$i$、$j$与其他客户延迟时间无关。

2. 交换后不增加$j$的延迟，但可能增加$i$的延迟。

3. $i$在$f_2$的延迟小于$j$在$f_1$的延迟。因此小于$f_1$的最大延迟$f$。

$i$在$f_2$的延迟不超过$j$在$f_1$的延迟

$delay(f_2,i)=s+t_j+t_i-d_i$

$delay(f_1,j)=s+t_i+t_j-d_j$

$d_j<d_i$

$delay(f_2,i)<delay(f_1,j)\le r$

小结

贪心法的正确性证明方法：交换论证

• 分析算法解与一般最优解的区别，找到把一般解改造成算法解的一系列操作（替换成份、交换次序）。

• 证明操作步数有限。

• 证明每步操作后的得到解仍旧保持最优。

得不到最优解的处理方法

• 输入参数分析

  考虑输入参数在什么取值范围内使用贪心法可以得到最优解。

• 误差分析

  估计贪心法——近似算法所得到的解与最优解的误差（对所有的输入实例在最坏的情况下误差的上界）。

找零钱问题

问题：设由$n$种零钱，重量分别为$w_1,w_2,...,w_n$，价值分别为$v_1=1,v_2,...,v_n$。需要付的总钱数是$y$。不妨设币值和钱数都为正整数。问：如何付钱使得所付钱的总重量最轻？

实例：$v_1=1,v_2=5,v_3=14,v_4=18,w_i=1,i=1,2,3,4. \\ y=28$

最优解：$x_3=2,\quad x_1=x_2=x_4=0$，总重为$2$。

建模

令选用第$i$种硬币的数目是$x_i,\quad i=1,2,3,...,n$

$\min \{\sum\limits_{i=1}^{n}w_ix_i\} \\ \sum\limits_{i=1}^{n}v_ix_i=y, \quad x_i \in N, \quad i=1,2,...,n$

动态规划算法

设$F_k(y)$表示用前$k$种零钱，总钱数为$y$的最小重量

$F_k(y)=\min\limits_{0\le x_k \le \lfloor \frac{y}{v_k}\rfloor}\{F_{k-1}(y-v_kx_k)+w_kx_k\}$

$F_1(y)=w_1\lfloor \frac{y}{v_1}\rfloor = w_1y$

贪心法

单位价值重量轻的货币优先，设

$\frac{w_1}{v_1} \ge \frac{w_2}{v_2} \ge ... \ge \frac{w_n}{v_n}$

使用前$k$种零钱，总钱数为$y$，贪心法的总重量为$G_k(y)$。

$G_k(y)=w_k\lfloor \frac{y}{v_{k}}\rfloor +G_{k-1}(y \mod v_k),\quad k>1$

$G_1(y)=w_1\lfloor \frac{y}{v_{1}}\rfloor =w_1y$

n=1，2贪心法是最优解

$n=1$，只有一种零钱，$F_1(y)=G_1(y)$

$n=2$，$x_2$越大，得到的解越好。

$\large F_2(y)=\min\limits_{0\le x_2 \le \lfloor y/v_2\rfloor} \{F_1(y-v_2x_2)+w_2x_2\} \quad \\ [F_1(y-v_2(x_2+\delta))+w_2(x_2+\delta)] \\ \quad - [F_1(y-v_2x_2)+w_2x_2] \\ = [w_1(y-v_2x_2-v_2\delta)+w_2x_2+w_2\delta] \\ \quad - [w_1(y-v_2x_2)+w_2x_2] \\ = -w_1v_2\delta+w_2\delta \\ = \delta(-w_1v_2+w_2)\le 0$

判别条件

定理：对每个正整数$k$，假设对所有非负数$y$有$G_k(y)=F_k(y)$，且存在$p$和$\delta$满足

$v_{k+1}=pv_k-\delta$，

其中$0\le \delta < v_k, v_k \le v_{k+1}$，$p$为正整数，

则下面的命题等价：

1. $G_{k+1}(y)=F_{k+1}(y)\quad$对一切正整数$y$；

2. $G_{k+1}(pv_k)=F_{k+1}(pv_k)$；

3. $w_{k+1}+G_k(\delta)\le pw_k$。

几点说明

• 根据条件1和3的等价性，可以对$k=3,4,...,n$，依次利用条件3对贪心法是否得到最优解做出判别。

• 条件3验证1次需要$O(k)$时间，$k=O(n)$，整个验证时间$O(n^2)$。

• 条件2是条件1在$y=pv_k$时的特殊情况。若条件1成立，显然有条件2成立。反之，若条件2不成立，则条件1不成立，钱数$y=pv_k$恰好提供了一个贪心法不正确的反例。

验证实例

例1：$v_1=1,v_2=5,v_3=14,v_4=18,w_i=1,i=1,2,3,4$。对一切$y$有

$G_1(y)=F_1(y),G_2(y)=F_2(y)$.

验证$G_3(y)=F_3(y)$

$v_3=pv_2-\delta \implies p=3,\delta =1. \\ w_3+G_2(\delta)=1+1=2 \\ pw_2=3 \times 1 =3 \\ w_3 + G_2(\delta) \le pw_2$

贪心法对$n=3$的实例得到最优解

---

例2 $v_1=1,v_2=5,v_3=14,v_4=18,w_i=1,i=1,2,3,4$.对一切$y$有

$G_1(y)=F_1(y),G_2(y)=F_2(y),G_3(y)=F_3(y)$,

验证$G_4(y)=F_4(y)$,

$v_4=pv_3-\delta \implies p=2,\delta = 10 \\ w_4 +G_3(\delta)=1+2=3 \\ pw_3=2 \times 1=2 \\ w_4+G_3(\delta) > pw_3$

$n=4,y=pv_3=28$，

最优解：$x_3=2$，贪心法：$x_4=1,x_2=2$。

小结

1. 贪心策略不一定得到最优解，在这种情况下有两种解决方法：

   • 参数化分析：分析参数取什么值可以得到最优解。

   • 估计贪心法得到的解在最坏情况下与最优解的误差。

2. 一个参数化分析的例子：找零钱问题。