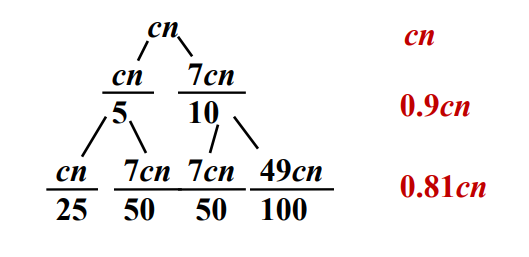分治策略-典型算法.md

选择问题

选最大和最小

输入：集合$L$（含$n$个不等的实数）

输出：$L$中的第$i$小的元素

• $i=1$，称为最小元素

• $i=n$，称为最大元素

位置处在中间爱你位置的元素，成为中位元素。

$n$为奇数，中位数唯一，$i=(n+1)/2$。

$n$为偶数，可指定为$i=n/2+1$。

选最大算法：顺序比较，在最坏情况下的时间为$W(n)=n-1$。

代码为：

def max_value(numbers: List[int]) -> Tuple[int, int]:
    if not numbers:
        return (-1, -1)
    if len(numbers) == 1:
        return (0, numbers[0])

    m = numbers[0], k = 0
    for i in range(1, len(numbers)):
        if m < numbers[i]:
            m = numbers[i]
            k = i
    return (k, m)

选最大最小通常算法：

• 比较算法，先选最大max

• 顺序比较，在剩余数组中选最小min，类似于选最大算法，但比较时保留最小值。

时间复杂度：$W(n)=n-1 + n-2 = 2n -3$

分组算法解决最大最小值：

输入：n个数的数组L

输出：max，min

1. 将n个元素两两一组分成$\lfloor n/2 \rfloor$组。

2. 每组比较，得到$\lfloor n/2 \rfloor$个较小和$\lfloor n/2 \rfloor$个较大的。

3. 在$\lceil n/2 \rceil$个较大（含轮空元素）找最大max

4. 在$\lceil n/2 \rceil$个比较（含轮空元素）中找最小min

时间复杂度：

• 在上述代码2中，组内比较$\lfloor n/2 \rfloor$次。

• 在3-4行内求max和min比较，最多$2 \times (\lceil n/2 \rceil - 1)$次。

• 即$W(n)=\lfloor n/2 \rfloor + 2 \times \lceil n/2 \rceil - 2 \\ = n + \lceil n/2 \rceil - 2 \\ = \lceil 3n/2 \rceil -2$

分治算法：

1. 将数组$L$从中间划分为2个子数组$L_1, L_2$

2. 递归地在$L_1$中求最大的$max_1$和$min_1$

3. 递归地在$L_2$中求最大的$max_2$和$min_2$

4. $max \gets \max{\{max_1, max_2\}}$

5. $min \gets \min {\{min_1, min_2\}}$

代码：

import math
from typing import List, Tuple


def max_min(arr: List[int]) -> Tuple[int, int]:
    i, j = 0, len(arr) - 1
    if i == j:
        return [arr[i], arr[i]]
    elif i == j - 1:
        return [arr[i], arr[j]] if arr[i] > arr[j] else [arr[j], arr[i]]
    else:
        mid = math.floor(j/2)
        max1, min1 = max_min(arr[i : mid])
        max2, min2 = max_min(arr[mid : j + 1])
        return [max(max1, max2), min(min1, min2)]

if __name__ == "__main__":
    arr = [6, 10, 32, 8, 19, 20, 222, 14, 53, 1]
    max_value, min_value = max_min(arr)
    print(max_value, min_value)  # 222, 1

最坏情况复杂度：

假设$\quad n=2^k, \\ \quad\quad W(n) = 2W(n/2) + 2 \\ \quad\quad W(2)=1$

解

$W(2^k) = 2W(2^{k-1}) + 2 \\ = 2 [ 2W(2^{k-2}) + 2] +2 \\ = 2^2W(2^{k-2})+2^2+2=... \\ 2^{k-1} + 2^{k-1} + ... + 2^2 + 2 \\ = 3 \times 2^{k-1} -2 =3n/2-2$

选择算法小结：

• 选最大：顺序比较，比较次数$n-1$

• 选最大最小：

  • 选择最大+最小，比较次数$2n-3$

  • 分组：比较次数$\lceil 3n/2 \rceil -2$

  • 分治：$n=2^k$，比较次数$3n/2-2$

选第二大问题

输入：$n$个数的数组$L$

输出：第二大的数$Second$

通常算法：顺序比较

1. 顺序比较找到最大的$max$

2. 从剩下$n-1$个数中找最大，就是第二大的$second$

时间复杂度：$W(n)=n-1+n-2=2n-3$ (比较次数)

提高效率的途径

• 成为第二大数的条件：仅在与最大数的比较中被淘汰

• 要确定第二大数，必须知道最大数

• 在确定最大数的过程中被记录下的最大数直接淘汰的元素

• 在上述范围内（被最大数直接淘汰的数）内最大数就是第二大数

(使用空间换时间)

锦标赛算法

1. 两两分组比较，大的进入下一轮，直到剩下1个元素$max$为止；

2. 在每次比较中淘汰较小的元素，将被淘汰元素记录在淘汰他的元素的链表上。

3. 检查$max$的链表，从中找到最大元素，即$secode$。

伪代码：

1. k <- n // 参与淘汰的元素数字

2. 将k个元素两两1组，分成$\lfloor k/2 \rfloor$组

3. 每组的2个数比较，找到较大数

4. 将被淘汰数记入较大数的链表

5. 如果 k 为奇数，那么 $k \gets \lfloor k/2 \rfloor + 1$

6. 否则 $k\gets \lfloor k/2\rfloor$

7. 如果$k>1$，那么转到步骤2

8. max $\gets$ 最大数

9. second $\gets$ max的链表中最大

其中，1-4是一轮淘汰，7为继续分组淘汰

时间复杂度分析：

命题1 设参与比较的元素有$t$个元素，经过$i$轮淘汰后元素至多为$\lceil t/2^i \rceil$。

证 对$i$归纳。$i=1$，分$\lfloor t/2 \rfloor$，淘汰$\lfloor t/2 \rfloor$个元素，进入下一轮的元素是$t - \lfloor t/2 \rfloor = \lceil t/2 \rceil$。

假设$i$轮分组淘汰后元素数至多为$\lceil t/2^i \rceil$，那么$i+1$轮分组淘汰后元素为：

$\lceil \lceil t / 2 ^ i\rceil / 2 \rceil = \lceil t/2^{i+1}\rceil$

命题2 $max$在第一阶段分组比较中总计进行了$\lceil \log n \rceil$次比较。

证 假设到产生$max$时总计进行$k$轮淘汰，根据 命题1 有$\lceil n/2^k \rceil = 1$。

若$n=2^d$，那么有$k=d=\log {n}=\lceil \log n \rceil$；

若 $2^d<n<2^{d+1}$ ，那么有$k=d+1=\lceil \log n \rceil$。

综上，

• 第一阶段元素数：$n$

  比较次数：$n-1$

  淘汰了$n-1$个元素

• 第二阶段：元素数$\lceil \log n \rceil$

  比较次数：$\lceil \log n \rceil - 1$

  淘汰元素数为$\lceil \log n \rceil - 1$

• 时间复杂度$W(n)=n + \lceil \log {n} \rceil -2$

第二大小结

求第二大算法：

• 调用2次找最大：$2n-3$

• 锦标赛算法：用空间换取时间。

一般选择算法的设计

问题：选第k小

输入：数组$S$，$S$的长度$n$，正整数$k，1\le k\le n$

输出：第k小的数

例子

• $S=\{3, 4, 8, 2, 5, 9, 18\}, k=4$，解：5

• 统计数据的集合$S，|S|=n$，选中位数，$k=\lceil n/2\rceil$

选择算法的分析

伪码

算法 Select(S, k)

1. 将S分成5个一组，共$n_M=\lceil n/5 \rceil$组

2. 每组排序，中位数防盗集合M

3. $m^* \gets Select(M,\lceil M/2 \rceil)$ // S分A，B，C，D

4. A,D元素小于 $m^*$ 放 $S_1$，大于 $m^*$ 放 $S_2$。

5. $S_1 \gets S_1 \cup C; \quad S_2 \gets S_2 \cup B$

6. if $k=|S_1| + 1$ then 输出 $m^*$

7. else if $k \le |S_1|$

8. then Select($S_1$,k)

9. then Select($S_2$,k-$|S_1|$-1)

用m*划分

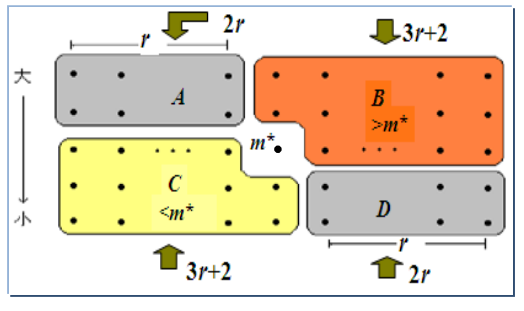
$\large n=5(2r+1),|A|=|D|=2r$

子问题规模至多：$\large 2r+2r+3r+2=7r+2$

子问题规模估计

不妨设$\large n=5(2r+1)$，$\large |A|=|D|=2r$，

$\large r=\frac{n/5-1}{2}=\frac{n}{10}-\frac{1}{2}$

划分后子问题规模至多为:

$\large 7r+2=7(\frac{n}{10}-\frac{1}{2}+2) \\ =\frac{7n}{10} - \frac{3}{2} < \frac{7n}{10}$

时间复杂度递推方程

算法工作量$W(n)$

行2：$O(n)$ // 每5个数找中位数，构成M

行3：$W(n/5)$ // M中找中位数$m^*$

行4：$O(n)$ // 用$m^*$划分集合S

行8-9：$W(7n/10)$ // 递归

$\large W(n) \le W(n/5) + W(7n/10) + O(n)$

递归树

$\large W(n) \le W(n/5) + W(7n/10) + O(n)$

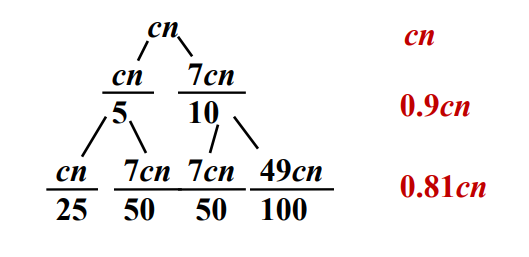
$\large W(n) \le cn(1+0.9+{0.9}^2+...)=O(n)$

讨论

为什么使用5个一组，而不是3个一组或者7个一组？

分析：递归调用

1. 求$m^*$的工作量与$|M|=n/t$相关，$t$为每组元素数，$t$大，$|M|$小。

2. 归约后子问题大小与分组元素数$t$有关，$t$大，子问题的规模大。

3分组时的子问题规模

假设$t=3$，3个一组：

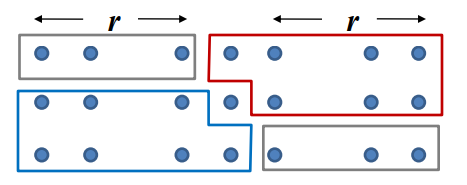
$n=3(2r+1) \\ r=(n/3-1)/2=n/6-1/2$

子问题规模最多为$4r+1=4n/6-1$

算法时间复杂度

算法时间复杂度满足方程：

$W(n)=W(n/3)+W(4n/6)+cn$

由递归树得到$W(n)=\varTheta (n \log n)$

关键点：

• $|M|$与归月后子问题规模值和小于$n$

• 递归树每行的工作量构成公比小于1的等比级数，算法的复杂度才是$O(n)$。