图的存储与算法
图论作为数学领域的重要分支已经有数百年的历史。图论应用的领域广泛,包括了地图、网页信息、电路、任务调度、商业交易、计算机网络和社交网络等。
图的类型
图是由一组顶点和一组能够将两个顶点相连的边组成的。
图有4种重要的模型:无向图(简单连接)、有向图(连接有方向性)、加权图(连接带有权值)和加权有向图(连接既有方向性又带有权值)。
特殊的图:
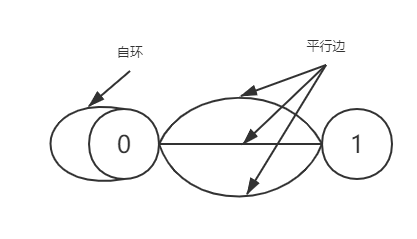
-
自环,即一条连接一个顶点和其自身的边
-
连接同一对顶点的两条边称为平行边。
术语
-
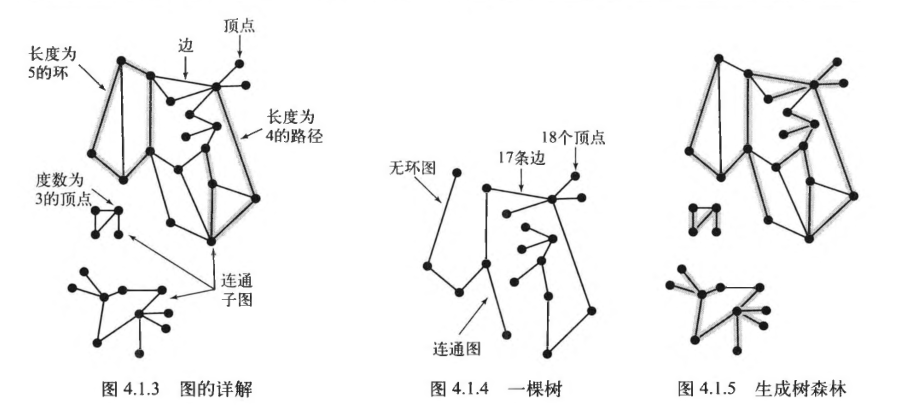
在图中,路径是由边顺序连接的一系列顶点。简单路径是一条没有重复顶点的路径。环是一条至少含有一条边且起点和终点相同的路径。简单环是一条(除了起点和终点必须相同之外)不含有重复顶点和边的环。路径或者环的长度为其所包含的边数。
-
如果从任意一个顶点都存在一条路径到达另一条任意顶点,我们称这幅图为连通图。一副非连通图的图由若干连通部分组成,他们都是其极大连通子图。
-
树是一副无环连通图。互不相连的树组成的集合叫做森林。连通图的生成树是它的一副子图,它含有图中所有的顶点且是一棵树。图的生成森林是它的所有连通子图的生成树的集合。
-
图的密度是指已经连接的顶点对占所有可能被连接的顶点对的比例。在稀疏图中,被连接的顶点对很少;而在稠密图中,只有少部分顶点之间没有边连接。
-
二分图是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
图的存储
图存储的要求:
-
它必须为可能在应用中碰到的各种类型的图预留出足够的空间;
-
Graph的实例方法的实现一定要快——它们是开发处理图的各种用例的基础。
图数据的存储方式有以下几种:
-
邻接矩阵
使用的布尔矩阵,当顶点
v和顶点w之间有相连接的边时,定义v行w列元素值为true,否则为false。优点是实现简单,缺点是空间复杂度高,为。 -
邻接表(链式存储)
以顶点为索引的列表数组,其中每个元素都对应一条链表,其中每个元素都是和该顶点相邻的顶点列表。
-
边集数组
使用
Edge类,它含有两个int实例变量。这种表示方法简洁但不满足第二个条件,实现adj()需要检查所有的边。 -
前向星
-
链式前向星
性能复杂度
| 数据结构 | 所需空间 | 添加一条边v→w | 检查w和v是否相邻 | 遍历v的所有相邻顶点 |
|---|---|---|---|---|
| 边的列表 | ||||
| 邻接矩阵 | ||||
| 邻接表 | ||||
| 邻接集 |
图的数据类型
相关API
| class | Graph | |
|---|---|---|
Graph(int V) |
创建一个含有V个顶点但不含有边的图 |
|
Graph(In in) |
从标准输入流in读入一幅图 |
|
int |
V() |
顶点数 |
int |
E() |
边数 |
void |
addEdge(int v, int w) |
向图中添加一条边v→w |
Itereable<Integer> |
adj(v) |
和v相邻的所有顶点 |
String |
toString() |
对象的字符串表示 |
toString()方法和adj()方法用来允许用例遍历给定顶点的所有相邻顶点(遍历顺序不确定)。
伪代码
-
计算
v的度数1
2
3
4
5int degree(Graph G, int v) {
int degree = 0;
for (int w: G.adj(v)) degree++;
return degree;
} -
计算所有顶点的最大度数
1
2
3
4
5
6
7
8
9int maxDegree(Graph G) {
int max = 0;
for (auto v = 0; v < G.V();v++) {
if (degree(G, v) > max) {
max = degree(G, v);
}
}
return max;
} -
计算所有顶点的平均度数
1
2
3double avgDegree(Graph G) {
return 2 * G.E() / G.V();
} -
计算自环的个数
1
2
3
4
5
6
7
8
9int numberOfSelfLoops(Graph G) {
int count = 0;
for (auto v=0; v<G.V(); v++) {
for (const auto w: G.adj()) {
int (v == w) count++;
}
}
return count/2; // 每条边被记过两次
} -
图的邻接表的字符串表示(
Graph的实例方法)1
2
3
4
5
6
7
8
9
10
11std::string toString() {
std::string s = V + " vertices, " + E + " edges\n";
for (auto v=0; v<V; v++) {
s += v + ": ";
for (const auto w: adj(v)) {
s += w + " ";
}
s += "\n";
}
return s;
}