算法数学基础 - 3

数列求和公式

等差、等比数列与调和级数

$\displaystyle\sum_{k=1}^{n}a_k=\frac{n(a_1+a_n)}{2} \\ \sum_{k=0}^{n}aq^k=\frac{a(1-q^{n+1})}{1-q}, \sum_{k=0}^{\infty}aq^k=\frac{a}{1-q}(q<1) \\ \sum_{k=1}^{n}\frac{1}{k}=\ln n+O(1)\\$

递推方程

设序列$a_0,a_1,\dots,a_n,\dots$简记为$\{a_n\}$，一个把$a_n$与某些个$a_i(i<n)$联系起来叫做关于序列$\{a_n\}$的递推方程。

迭代法求解递推方程

迭代法：

• 不断用递推方程的右部替换左部

• 每次替换，随着$n$的降低在和式中多出一项

• 直到出现初值停止迭代

• 将初值并入对和式求和

• 可用数学归纳法验证解的正确性

换元迭代：

• 将对$n$的递推式换成对其他变元$k$的递推式

• 对$k$直接迭代

• 将解（关于$k$的函数）转换成为关于$n$的函数

差消法化简高阶递推方程

递归树

递归树：

• 递归树是迭代计算的模型；

• 递归树的生成过程与迭代过程一致；

• 递归树上所有恰好是迭代之后产生和式中的项；

• 对递归树上的项求和就是迭代后方程的解。

迭代在递归树中的表示

如果递归树某结点标记为$W(m)$，

$W(m)=W(m_1)+\dots+W(m_t)\\ +f(m)+\dots+g(m), m_1,\dots,m_t<m$

其中，$W(m_1),\dots,W(m_t)$称为函数项。

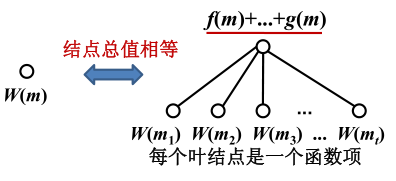
递归树的生成规则

• 初始，递归树只有根节点，其值为$W(n)$

• 不断继续下述过程：

  • 将函数项叶节点的迭代式$W(m)$表示成二层子树

  • 用该子树替换该叶节点

• 继续递归树的生成，直到树中无函数项（只有初值）为止。

主定理及其证明

主定理的应用背景

求解地推方程

$T(n)=aT(n/b)+f(n)$

• $a$ ： 归约后的子问题个数

• $n/b$：归约后子问题的规模

• $f(n)$：归约过程及组合子问题的解的工作量

二分检索：$T(n)=T(n/2)+1$

二分归并排序：$T(n)=2T(n/2)+n-1$

主定理：设$a\ge1,b>1$为常数，$f(n)$为函数，$T(n)$为非负整数，且$T(n=aT(n/b)+f(n)$，则

1. 若$f(n)=O(n^{\log_ba-\epsilon}),\epsilon>0$，那么$T(n)=\Theta(n^{\log_ba})$

2. 若$f(n)=\Theta(n^{\log_ba})$，那么$T(n)=\Theta(n^{\log_ba}\log n)$

3. 若$f(n)=\Omega(n^{\log_ba+\epsilon},\epsilon>0)$，且对于某个常数$c<1$和充分大的$n$有$af(n/b)\le cf(n)$，那么$T(n)=\Theta(f(n))$

主定理的应用

求解递推方程

1. 求解递推方程$T(n)=9T(n/3)+n$

   解 递推方程中的 $a=9,\quad b=3,\quad f(n=n)$

   $n^{\log_39}=n^2,\quad f(n)=O(n^{log_39-1})$

   相当于主定理case1，其中$\epsilon =1$

   根据定理得到 $T(n)=\Theta(n^2)$

2. 求解递推方程 $T(n)=T(2n/3)+1$

   解 上述递推方程中 $a=1, b=3/2,f(n)=1,n^{\log_{3/2}1}=n^0=1$

   相当于主定理的Case2，

   根据定理得到$T(n)=\Theta(\log n)$

3. 求解递推方程 $T(n)=3T(n/4)+n\log n$

   解 上述递推方程中的 $a=3,b=4,f(n)=n\log n$

   $n\log n=\Omega(n^{\log_43+\epsilon})=\Omega(n^{0.793+\epsilon})$

   取$\epsilon=0.2$即可。

条件验证：

要使$af(n/b)\le cf(n)$成立，代入$f(n)=n\log n$，得到

$3(n/4)\log(n/4)\le cn\log n$

只要$c\ge 3/4$，上述不等式可以对所有充分大的$n$成立。相当于Case3。

因此有 $T(n)=\Theta(f(n))=\Theta(n\log n)$

递归算法分析：

• 二分搜索

  $W(n)=W(n/2)+1,W(1)=1\quad a=1,b=2,n^{\log_21}=1, f(n)=1$，

  属于Case2，$W(n)=\Theta(\log n)$

• 二分归并排序

  $W(n)=2W(n/2)+n-1, W(1)=0, \quad a=2,b=2,n^{\log_22}=n,f(n)=n-1$

  属于Case2，$W(n)=\Theta(n\log n)$

不能使用主定理的例子：

求解 $T(n)=2T(n/2)+n\log n$

解：$a=b=2,n^{\log_ba}=n,f(n)=n\log n$

不存在$\epsilon >0$ 使右式成立 $n\log n = \Omega(n^{1+\epsilon})$，

不存在$c<1$使$af(n/b)\le cf(n)$对所有充分大的$n$成立

$2(n/2)\log(n/2)=n(\log n-1)\le cn\log n$

递归树求解：

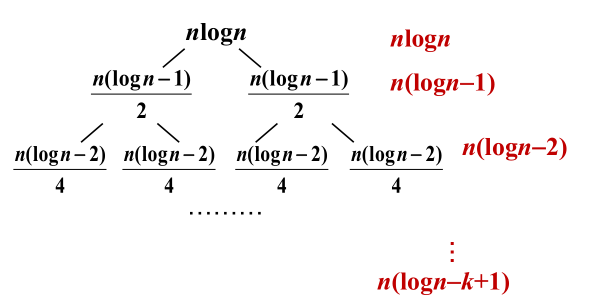
$T(n) = n\log n+ n(\log n-1)+ n(\log n-2) \\ + \dots +n(\log n-k+1) \\ = (n\log n)\log n - n(1+2+\dots+k-1) \\ = n\log^2n-nk(k-1)/2 = O(n\log^2n)$

// todo: 继续阅读《具体数学》第一章递推式与第二章和式。