Social computing 6 —— 网络流量的博弈
网络流量的博弈
-
网络结构上的博弈
- 公路交通网
-
网络中的博弈
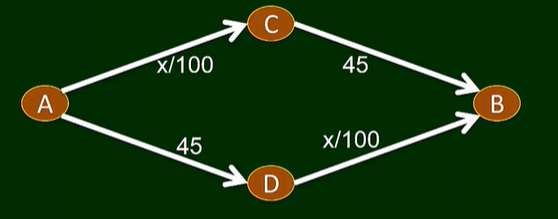
假设有4000辆车,都要从A走到B
-
参与人: 4000位司机
-
策略选择:ACB 或 ADB
-
回报:行驶时间(越小越好),显然也取决于他人的策略
“均衡” = 没人通过改变选择可以得到更好的回报
均衡:上下路各有2000辆车;对于每辆车而言,对应回报为65。
此时,若某人要改变,则他的行驶时间为 ,因此无人改变
假设,C→D之间修一条快速路,则
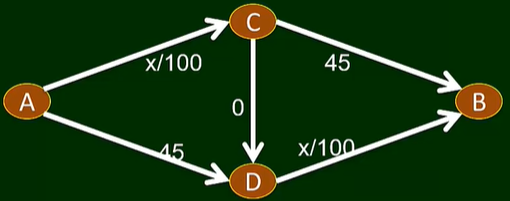
若大家都走:A → C →D→B,则每个人的行驶时间为
-
注意,在没修这条路之前,均衡中每个人行驶时间为65
-
如果某人打算改变为A→D→B,则他的行驶时间将变为,于是他不会改变!
→ 布雷斯悖论
为什么大家不能像从前那样?
-
你会很合理地想走A→C→D→B,也就是说,从前那样的交通模式是不均衡的。
-
你会这么想,其他人呢?
-
-
小结
-
通过一种简单的交通网络模型,我们看到“在网络上的博弈”的一种范式,特别是结构对均衡的影响。
-
我们看到了“布雷斯悖论”的出现,它其实可以看成是我们现实生活中有时看到“投入资源反而使情况更糟糕”情形的一种简单化、但有效的解释。
-
这个例子也告诉我们,在现实生活中,参与一个博弈,可能是无形中的。
-
布雷斯悖论的一般性
布雷斯悖论(Braess’s paradox)指的是一个交通网络上增加一条路反而是网络上的旅行时间增加。
例子:
-
高速公路免费带来的影响
-
2012年中秋开始,政府颁布一项惠民政策,即:
-
在法定节假日,高速公路免费通行。
-
每年中国高速公路公司将因此减收200亿人民币,与此同时免费政策也引发各方争议:
免费带动了消费额,远远大于高速公路公司的减收。
免费也带来了高速公路的拥堵,旅游景点的人流饱和等。
-
-
高速公路免费带来影响的理论化
-
与布雷斯悖论不同的地方在于,除了结构与流量关系之外,这个例子涉及多个行动者:
- 高速公路公司、车主及其家庭、政府
-
简化模型
-
免费政策 = 多修了一条公路
-
通行时间 = 交通总成本,包括时间和费用
-
-
布雷斯悖论的一般化
-
如此,我们是不是看到了另一种形态的布雷斯悖论
-
虽然也是交通网络,却是另一种形态
-
-
-
探讨
-
通行时间 - 流量 - 成本 - 社会成本
-
布雷斯悖论的含义是,通过网络结构的变动,意在改善交通行动,结果是导致了更加糟糕的交通。
-
中国高速公路免费所产生的效应,看起来类似
-
那么我们是否可以把布雷斯悖论做进一步抽象?譬如说
-
“好心办坏事”,意在增加社会福利的行动,反而增加了社会成本
-
例如:
-
意在改善儿童教育机会的制度变动,其结果是对学校需求的更加不平衡,有些学校无人问津,有些学校则挤破脑袋
-
同样,改善就医便利程度和降低个人就医负担的制度变动,其结果不仅是就医总费用急剧增加,对医院的需求更加不平衡,高等级医院挤破脑袋,社区医院门可罗雀。
-
-
-
-
小结
-
布雷斯悖论是社会政策、公共服务中可以意会到的现象
-
意会与科学论证,是两回事,对布雷斯悖论的推广,应该还是一个可探索的领域。
-
拍卖的意义及其形式
-
拍卖的普遍性
-
拍卖(auction)是很典型的节点之间的互动,例
-
佳士得、苏富比拍卖艺术品
-
政府拍卖土地、车牌
-
毕业摆摊,买旧物
-
-
竞标(bidding)也是一种拍卖
- 卖家将合同机会进行拍卖
-
-
拍卖的意义
-
拍卖是普遍存在的经济互动形态
- 模式简单,互动却复杂
-
也是博弈论应用的典型场景
-
参与者:参加拍卖的人,买卖双方,相当于两方博弈
-
策略:出价
-
收益:对物品的估值(支付价格)或为零,即不成交;对卖家而言,就是其得到的支付价格,或为零。
-
均衡:即在该状态下所有参与者的策略互为最佳应对,任何个人都没有理性的冬季来改变自己的策略,在拍卖中如何体现?
-
-
-
拍卖的形式
-
在拍卖中,均衡是拍卖规则下的均衡,因此拍卖规则或拍卖形式,对均衡的达成有直接影响。
-
最简单的,单品拍卖。
-
英式拍卖 (古董艺术品的拍卖)
也称为“出价逐升式拍卖”,是目前最流行的网上拍卖方式。拍卖中,竞买人出价由低开始,此后出价一个比前一个要高,直到没有更高的出价为止,出价最高即最后一个竞买人将以其所出的价格获得该商品。
既然获胜的竞买人的出价只需比前一个最高价高一点,那么每个竞买人都不愿马上按照其预告价出价。当然,竞买人也要冒风险,他可能会被令人兴奋的竞价过程吸引,出价超出了预估价,这种心理现象被称为赢者诅咒(Winner’s Curse)。
-
荷兰式拍卖(农产品)
是英式拍卖的逆行,也称为“出价逐降式拍卖”。它是先由拍卖人给出一个潜在的最高价,然后价格不断下降,直到有人接受价格。该方式的缺点是拍卖速度太快,而且需求所有竞买人在某一时候竞买。
-
密封拍卖(Sealed Auction) (适合招标、互联网广告)
是指竞买人通过加密的E-mail将出价发送给拍卖人,再由拍卖人统一开标后,比较各方递价,最后确定中标人。
密封拍卖可分为一级密封拍卖和二级密封拍卖。一级密封拍卖也称为密封递价最高价拍卖,即在密封递价过程中,出价最高的竞买人中标。如果拍卖的是多件相同物品,出价低于前一个的竞买人购得剩余的拍卖品。二级密封拍卖也称为密封递价次高价拍卖,其递价过程与一及密封拍卖类似,只是出价最高的竞买人是按照出价第二高的竞买人所出的价格都按其预告价出价,降低了竞买人串通的可能性,获胜者不必按照最高价付款,从而使所有的竞买人都想以比其一级密封拍卖中高一些的价格出价。威廉.维克瑞(William Vickrey)因对此拍卖的研究而荣获1996年诺贝尔经济学奖,因此,二级密封拍卖也称为维氏拍卖。
-
双重拍卖(double auction)
Open-outcry double auctions(开放出价双重拍卖)
Sealed-bid double auctions(密封递价双重拍卖)
-
-
次价支付
-
假设有一件物品
不同人对其价值有不同的看法,v1, v2, v3, … , vk
每个人都有一个竞价:b1, b2, b3, … , bk
则 就是 i 可能得到的收益
-
次价拍卖规则
出价最高者得到购买权,但只需支付(b中的)次高价
-
-
出价策略
-
如果大家都按照自己真实的估值出价
则没有人能通过改变,获得更大的回报;这种情况下,大家互为最佳应对,均衡;尽管改变出价可能得到同样的回报
-
如果某个人不按照自己真实的估值出价
其他人按照估值出价,则他的回报要么没变化,要么变少,总之不可能获得更好的回报
-
因此“次价出价”是鼓励买家按照自己的真实估值出价
-
-
真的吗?
-
提高报价,只是当超越其他人报价才有差别,但在这种情况下,就要支付比估值多的钱 —— 亏了
-
真实报价
-
降低报价。只是当低于其他人的报价才有差别,但这种情况下,就得不到交易权,因此没意义了。
-
-
-
拍卖规则要点
-
成交规则,谁获得拍品?
通常是报价最高者或最低者。
-
支付价格,首价或次价
次价规则的引入,对于竞拍者的出价策略是有影响的。
-
是否知道他人出价
-
密封拍卖是不知道的,需要竞价者做出独立判断,且是否竞得,只有一次机会
-
非密封拍卖,知道他人竞价,且会受到他人出价的影响
-
-
-
小结
-
日常生活中,拍卖是随时发生的现象,对于我们理解博弈论的应用是一个难得的典型情景。
-
拍卖的形式多种多样,简单的、复杂的拍卖,从出价方式来看,有增价、降价、密封,三种形式;从支付方式看,有首价、次价两种方式。
-
拍卖中的博弈与占优策略
-
密封报价拍卖的两种形式
-
首价密封拍卖(FPA)
最高报价者得到交易权,支付最高报价。
-
次价密封拍卖(SPA)
最高报价者得到交易权,支付次高报价。
-
-
次价密封拍卖问题
-
一件物品
-
估值,不同的人对它的价值有不同的认识(即底价,最多愿意花的钱),v1,v2,… ,vk
-
每个人提出一个竞拍价, b1 > b2 > … > bk
-
次价拍卖规则:出价最高者得购买权,但只需支付(b中)第二高的出价,即 是出价最高者参与人得到的收益,其他人为0。
-
-
什么策略最优?
博弈论视角(占优策略):不可能通过改变其他策略得到更大的回报,无论别人出价策略如何。
回报: 估值 - 付出
结论:按照自己的估值出价最优!(非严格占优策略)
-
论证
假设在一次拍卖活动中,你认为拍品的估值最多为100元,你也考虑出价100元,现在考虑你能否通过不同的出价获得较大的回报
-
第一,你获得交易权。此时,你有正回报
-
提高报价也不会改善回报
-
降低报价,若不低于第二个人的,也不会改善回报,若低于第二个人的,则失去交易权,回报变成0(变少了)
-
-
第二,你没有获得交易权(有人出价x > 100),此时,你的回报为0。
-
降低报价不会改变回报。
-
提高报价,若不高于第一个人的报价,也不会改善回报。若高于第一个人的,你赢得了交易权,但要支付原来第一个人的报价(高于你的估值),于是回报为负(减少了)
-
-
-
小结
-
采用次价密封拍卖的规则,拍卖一件物品,对参拍人来说,按照估值报价是占优策略
-
现实中,参拍人自觉应用这个结论的困难自安于每个人其实很难知道自己对一件物品的“估值”到底是多少
-
“估值” ≠ “我愿意出的钱数”
-
“估值” = “我绝不接受高于这个钱数”
-
-
-
首次密封拍卖没有这个性质
-
匹配问题
2012年度诺贝尔经济学奖得主是劳埃德·夏普利和艾文·罗斯,两人研究市场制度下参与者之间如何达成配对的理论和实践问题,其中“GS算法”有重要地位。
学生必须合适的学校匹配,需要移植器官的患者必须与器官捐赠者匹配。这样的匹配如何才能尽可能高效的完成?什么样的方式对哪一方更有利?劳埃德•夏普利采用所谓的“合作博弈”理论去研究和比较不同的匹配方法。“求解”的难点在于确保匹配的结果是稳定的这一突出贡献,也就是说,两个代理人无法找到对方在当前情况下条件优于自己地方。而且,夏普利和他的同事创造了具体的方法即——Gale-Shapley algorithm来确保匹配是稳定的。这些方法也限制了代理人操纵匹配过程的动机。
艾文•罗斯认识到,Shapley值的理论结果可以解释在实践中重要市场的功能。通过一系列的实证研究,罗斯和他的同事证明,稳定是特定的市场机构成功的关键。罗斯后来在系统实验室中的实验都证实这一结论。他还帮助重新设计现有的医院和医生,学校和学生,器官捐献者与患者进行稳定匹配的机制。这些改革都基于Gale-Shapley算法,且考虑到具体情况和道德限制,如排除了侧面支付等问题,使得这一机制更有可操作性。
匹配是人类社会中常见的基本问题之一,会出现在各种不同的背景下。
-
匹配市场问题框架

卖方,买方,估值矩阵
-
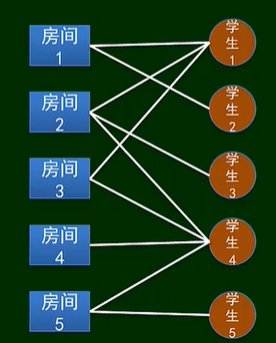
简单匹配问题
-
二部图是表达这种供需关系的工具
-
问:是否存在一种安排(配置)使得每个人都满意?
二部图中完美匹配:一组边,覆盖了所有的节点,没有节点冲突
-
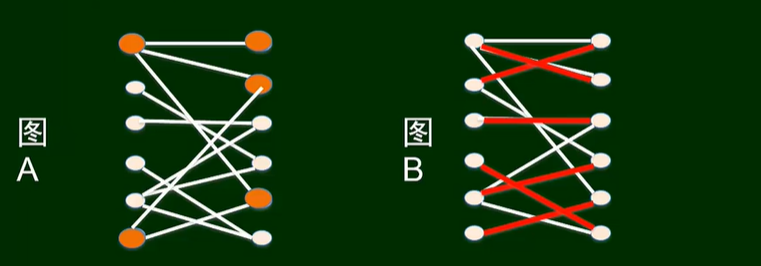
这两个图体现的要求能否被满足?
-
不能满足 = 存在受限组;S, N(S)
-
能被满足 = 存在完美匹配
-
-
-
基于估值的匹配问题
-
人们表达偏好不一定就是”要“与”不要“,对于不同的物品,可以有多样性的估价值判断
-
同一个物品,不同的人,估值可能不同
-
同一个人,不同的物品,估值可能不同
-
-
如何在”人“和”物品“之间配置(匹配)?
-
-
如何评估一种安排的好坏?
在经济学中,社会福利 = 参与人收益综合
社会最优:收益综合最大
-
小结
-
匹配问题描述的基本框架,参考上面的图
-
通过简单匹配问题,引入供需关系之间的二部图表达方式
-
不同供需配置方案的优劣比较指数 —— 社会福利,以及对“社会最优”性质的认识
-
匹配问题的解
-
利用收益矩阵计算
-
偏好卖家图(市场经济原则,涨价)
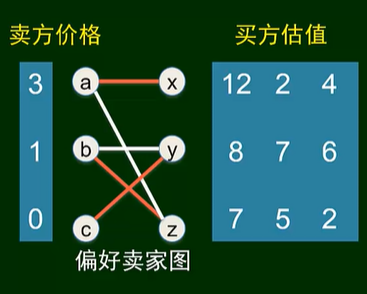
-
匹配问题的解
-
“计划经济”: top-down,从宏观结果到具体安排
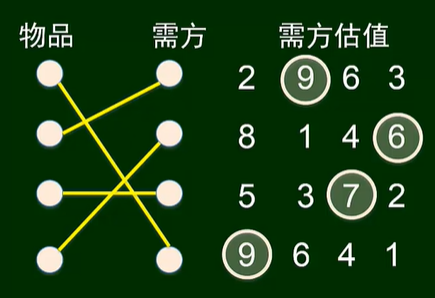
-
市场经济思路
-
引入价格机制,让需求方选择(博弈),看最后能否达到宏观最优的结果。
-
清仓价格:每个需求方都能无冲突地得到最大的收益(差价)
? 清仓价格同时也导致社会福利最大?
-
-
清仓价格 → 最大的 ∑ 估值
∑ 收益(差价) = ∑估值-∑价格
-
考虑清仓价格,以及偏好卖家图中的完美匹配对应的配置(M)
每一个收益都是最大 → “∑收益”最大 → “∑估值”最大
-
-
-
小结
-
以匹配问题为背景,比较“计划经济”与“市场经济”思路
-
简单模型,体现要点
-
“市场无形之手”含义与优势的一种解释
-
参考
Social computing 6 —— 网络流量的博弈