Social Computing 4 —— 万维网结构、链接分析与网络搜索

一、有向图

有向图是指一个有序$(V(D), E(D), \Psi(D))$，其中$\Psi(D)$是关联函数，它使得$E(D)$中的每一个元素（称之为有向边或弧）对应于$V(D)$中的一个有序元素（称为顶点或点）对。

出度与入度 设$D$是一个有向图，$D$中的顶点$v$的入度$d_D^-(v)$是指以$v$为头的弧的数目，$v$的出度$d_D^+(v)$是指以$v$为尾的弧的数目，$v$的度$d_D(v)$则是出度和入度之和，我们用$\delta^-(D)$和$\Delta^-(D)$和$\delta^+(D)$和$\Delta^+(D)$分别表示$D$中顶点的最小和最大入度、最小和最大出度，并使用$\delta(D)$和$\Delta(D)$分别表示$D$中的顶点最小度和最大度，并用$v(D)$，$\varepsilon(D)$来源表示$D$中的顶点数和弧数。

孤立点 $V$中不与$E$中任一条边关联的点成为$D$的孤立点。

简单图 不含平行边的图。

完备图 图中任何两个顶点$U$和$u$之间，恰有两条有向边$(u, v)$及$(v, u)$，则称该图为有向图$D$的完备图。

基本图 把有向图$D$的每条边出去定向就得到一个相应的无向图$G$，称$G$为$D$的基本图，称$D$为$G$的定向图。

强连通图 给定有向图$G=(V, E)$，并且给定向图$G$中的任意两个节点$v$和$u$，如果节点$u$和$v$相互可达，即至少存在一条路径可以由节点$u$开始，到节点$v$终止，同时存在至少一条路径可以由节点$v$开始，到节点$u$终止，那么就称该有向图$G$是强连通图。

弱连通图 若至少有一对节点不满足单向连通，但去掉边的方向后从无向图的观点看是连通图，则$D$称为弱连通图。

单向连通图 若每对节点至少有一个方向是连通的，则$D$称为单项连通图。

强连通分支 有向图$G$的极大强连通子图称为该有向图的强连通分支。

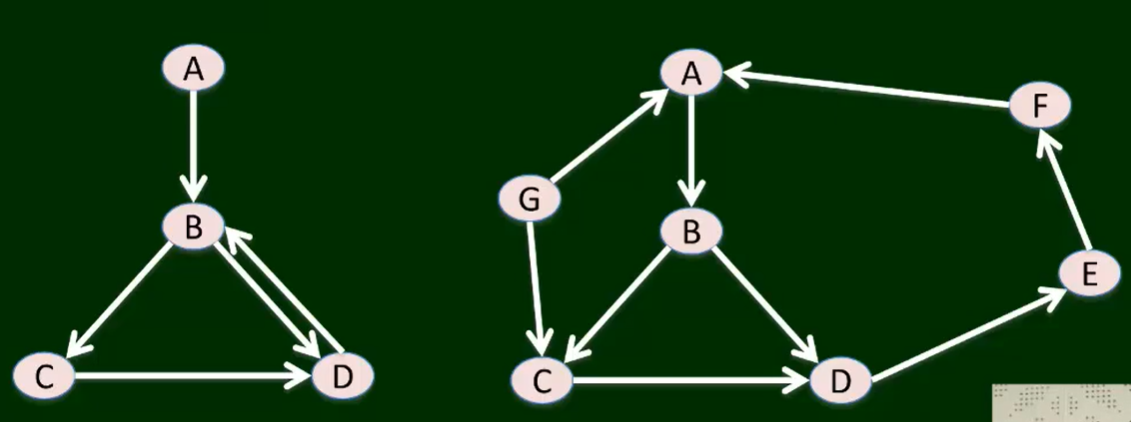
• 出度与入度：

  如上图中右图，节点B的出度为2，入度为1。

• 有向路径：

  • 从x到y有一条有向路径，不一定从y到x存在有向路径；

  • 即使从x到y有，从y到x也有，但这两条路径经过的节点可能完全不同。

    A → B ; B → D → E → F → A

• 有向图的强连通性

  • 强连通分量

    一个节点子集和它们之间的边，满足：

    • 第一，如果它有两个或者更多的节点，那么其中任意两个节点之间的都存在两个方向上的有向路径；

    • 第二，不被包含在一个更大得且满足第一个要求的节点集合之中。

  • 尽可能大的双向连通节点子集

    

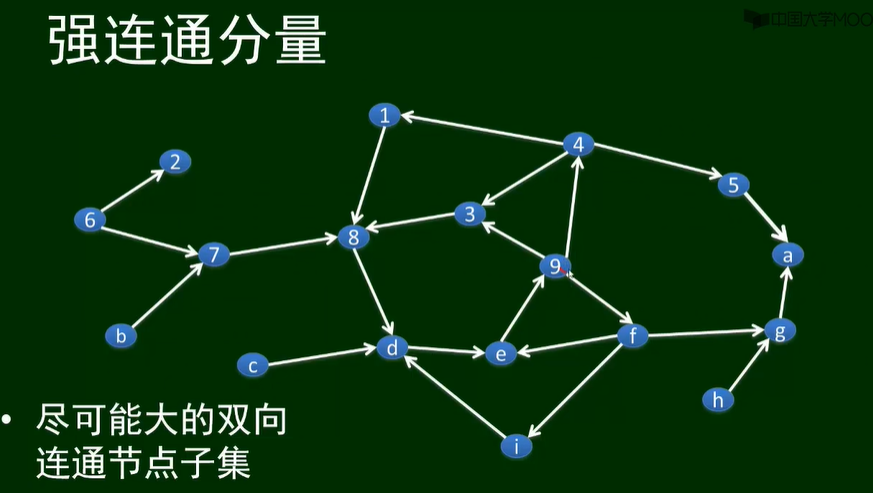
  • 在一个有向图中，不可能存在一个节点属于两个不同的强连通分量。

总结：

• 有向图是描述具有方向性关系的工具。

• 与（无向）图的几个基本概念的对应关系：

  节点 —— 节点

  边 —— 有向边

  路径（圈） —— 有向路径（有向圈）

  连通 —— 强连通

  连通分量 —— 强连通分量

二、将Web看成是一个有向图

领结：Web信息结构的一种概貌

• Andrei Broder等发现万维网包含一个超大强连通分量SCC，加上其他部分，显示出一种形象的结构

  • 链入，链出，卷须（管道），游离

  • SCC

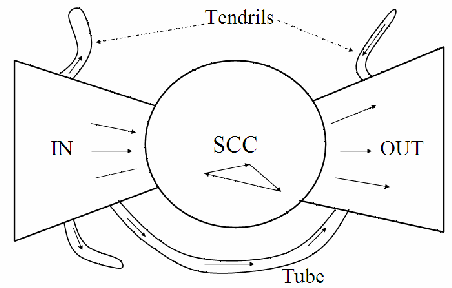
    Furthermore, several studies have suggested that the directed graph connecting web pages has a bowtie shape: there are three major categories of web pages that are sometimes referred to as IN, OUT and SCC. A web surfer can pass from any page in IN to any page in SCC, by following hyperlinks. Likewise, a surfer can pass from page in SCC to any page in OUT. Finally, the surfer can surf from any page in SCC to any other page in SCC. However, it is not possible to pass from a page in SCC to any page in IN, or from a page in OUT to a page in SCC (or, consequently, IN). Notably, in several studies IN and OUT are roughly equal in size, whereas SCC is somewhat larger; most web pages fall into one of these three sets. The remaining pages form into tubes that are small sets of pages outside SCC that lead directly from IN to OUT, and tendrils that either lead nowhere from IN, or from nowhere to OUT. Figure 19.4 illustrates this structure of the Web.

    source： https://nlp.stanford.edu/IR-book/html/htmledition/the-web-graph-1.html

• 如何按照”领结“思路，获得一个有向图的几个组成部分？

  

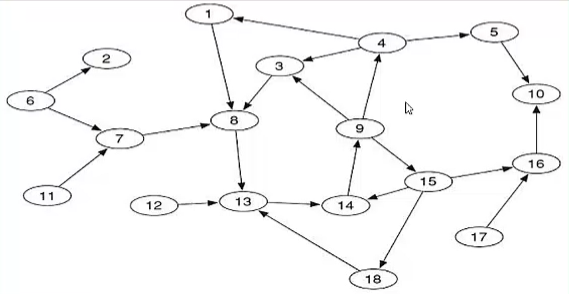
  • 简化：只关心SCC，IN和OUT三个部分

  • 假设我们知道某个节点一定在SCC中

  • 给定有向图和其中的一个节点，如何得到包含该节点的强连通分量（SCC），以及相对于这个强连通分量的IN部分和OUT部分。

  从某一节点上做广度优先搜索，从$1$节点进行搜索：

  $FS = \{ 1, 8, 13, 14, 9, 3, 4, 15, 5, 16, 18, 10\}$

  然后，在依据反向图进行搜索：

  $BS=\{1, 4, 9, 14, 13, 15, 8, 12, 18, 3, 7, 6, 11\}$

  所以，$SCC = FS \cap BS = \{1, 3, 4, 8, 9, 13, 14, 15, 18\}$

  $IN = BS - SCC = \{6, 7, 11, 12\}$

  $OUT = FS - SCC = \{5, 10, 16\}$

• 有向图的“领结”表示

  

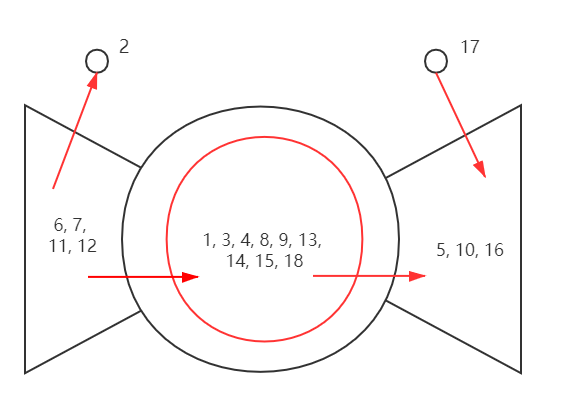
总结：

• 有向图是一种信息组织的有效形式

• 将Web看成是一个有向图，人们发现它宏观上像一个“领结”，多次数据实验验证了这个结论。（IN, OUT, SCC）

• 广度优先搜索，视具体得到“领结”的各个组成部分的基本手段。

三、中枢与权威

搜索引擎关心的基本问题

• 计算机显示屏只能够显示5-6个结果，典型搜索引擎掌握的网页超过60亿

• 对用户提交的一个查询，如何从这种海量网页集合中将最可能满足用户需求的少数几个结果找出来，展现在计算机显示屏上？

传统信息检索（IR）技术要点

• 基于词语之间的相关性（relevance）

• 传统应用背景

  • 文档集合：图书，规范的文献

  • 查询：主题词，关键词

  • 查询意图：获取与查询词有关的书籍和文章

  • 用户：图书管理人员

• ”查询目标包含查询词“ 是一个合理假设

  • 在形成查询词的时候就有这样的意识

有效利用链接关系蕴含的信息，是搜索引擎超越传统信息检索系统、技术进步的重要标志。

• Web page之间的链接有两层含义：关系、描述

反复改进原理 （principle of repeated improvement）

网页的“中枢”与“权威”性

• 万维网中一篇网页的两面属性。

  观念：

  • 被很多网页指向：权威性高，认可度高

  • 被指向很多网页：中枢性强

• HITS算法：计算网页的权威值（auth）和中枢值（hub）

  • Hyperlink-Induced Topic Search

$auth(p)$ 和 $hub(p)$ 的计算方法

• 输入： 一个有向图

• 初始化：对于每一个节点 p，$auth(p) = 1, hub(p) = 1$

• 利用中枢值更新权威值

  • 对于每一个节点 p，让$auth(p)$等于指向 p 的所有节点 q 的$hub(q)$之和

• 利用权威值更新中枢值

  • 对于每一个节点 p，让$hub(p)$等于 p 指向的所有节点 q 的$auth(q)$之和

• 重复上述步骤若干（k）次

  在搜索引擎领域，auth值或hub值高的网页，分别称为“权威网页”和“中枢网页”。一篇网页可以兼具二者。

• 归一化与极限

  • 数值随迭代次数递增

  • Auth 和 hub 值的意义在于相对大小

  • 在每一轮结束后作归一化：$值/总和$

  • 归一化结果随迭代次数趋向于一个极限

    • 相继两次迭代的值不变

    • 极限与初始值无关，即存在“均衡”

总结：

• 在一个由“引用”或者“推荐”关系构成的信息网络中，每个节点都有两种自然作用：“权威”与“枢纽”（中枢）

• 这样的作用可以用过“HITS算法”得到量化

• HITS算法的基本精神是基于信息网络的结构，在两个量之间交叉进行“反复改进”

四、PageRank： 节点重要度的一种测度

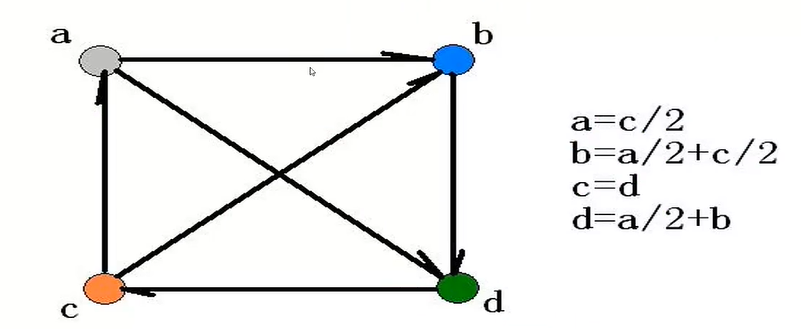
基本要领：每一个节点将自己的值均分给出向邻居，每个节点将从入向邻居收到的值加起来。

PageRank算法基本描述：

• 输入： 一个有$n$个节点的网络（有向图），设所有节点的 pagerank 初始值为 $\frac{1}{n}$。

• 选择操作的步骤数$k$。

• 按照下列规则，同时对每个节点进行操作，做$k$次：

  • 每个节点将自己当前的 pagerank 值通过出向链接均分传递给所指向的节点

    若没有出向链接，则认为传递给自己（或者说保留给自己）

  • 每个节点以从入向链接获得的（包括可能自传的）所有值之和更新它的 pagerank

总结：

• 在一个由“引用”或者“推荐”关系构成的信息网络中，每个节点的重要性可以认为取决于有多少人推荐，以及推荐人的重要性

• 这种重要性可通过“PageRank算法“得到量化

• PageRank算法的基本精神是基于信息网络的结构，让每个节点不断把自己的重要性分给出向邻居，同时用从入向邻居收到的重要性之和来更新自己。

五、同比缩减与等量补偿

PageRank基本算法在某些结构上的“病态”

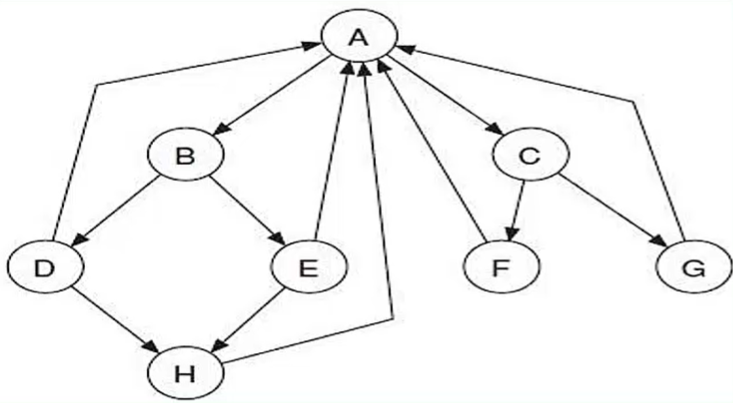
从上图去掉$(G, A)$和$(F, A)$ 边，添加 $(F, G)$ 和 ${G, A}$ 两条边，得到：

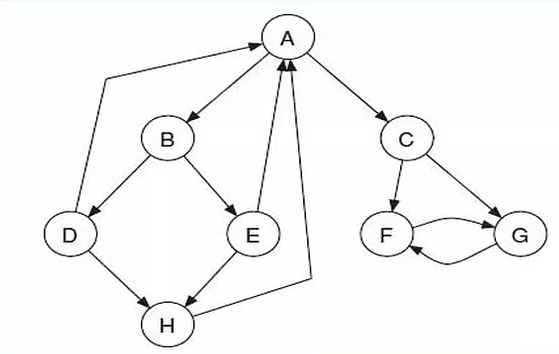
此时，F 和 G两个节点显得很“自私”：不断吸收其他节点的价值，但不向外分享。

PageRank的同比缩减与统一补偿原则

• 同比缩减

  在每次运行基本PageRank更新规则后，将每一个节点的PageRank值都乘以一个小于1的比例因子$s (0<s<1)$，经验值在0.8~0.9之间。

• 统一补偿

  在每一个节点的PageRank值上统一加上$\frac{1-s}{n}$。

这样，既维持了$\sum PR = 1$的性质，也防止了PR值过度集中到个别节点。

随机游走：PageRank的另一种等价理解

• 想象一个人从一篇随机选择的网页开始，然后随机选择其中的链接浏览到下一篇网页，并不断如此进行，称为“随机游走”。

• 考虑任意一篇网页X，问：经过k步随机游走到达X的概率是多少？

• 可以证明：到达X的概率等于运行PageRank基本算法k步得到的值。

• 随机游走概念稍加修改也可以和同比缩减、统一补偿的PageRank等价。

总结：

• 信息一旦刻画成一种网络，其中的边经常自然地隐含着一种“推荐”或者“引用”关系，人们可以利用这种关系对信息的作用进行评估：

  • 影响力、重要性、权威性、新颖性……

• 先进的评估方法不仅考虑局部结构，而且会考虑全局结构带来的影响（节点特征性质在网络中的传播）

• HITS算法、PageRank算法

• 当理想遇到现实 —— 重要现实情况的处理

  • 数据范围问题，退化网络结构问题