Social Computing 3 —— 小世界实验及其惊奇

小世界问题 The Small-World Program

1. S. Milgram (1967) 实验

   • 现象：俗语 “My it’s a small world.”

   • 问题：两个互不相识得人，如果想认识，中间需要经过几个人

   • 意义： a certain mathematical structure in society

   • 假设

     • 由于每个人都有熟人，熟人之间没有芥蒂，可以交往。故，不曾有连接的两个人之间，如果要建立连接，中间人的数量应该不多。

     • 每个人的确都有熟人，不过，不同类型或阶层熟人之间，不会有交往。故，不曾有连接的两个人之间，不可能建立连接

   • 设计

     • 选择一个随机起点，观察需要经过多少个中间人，能够到达目标点

   • 规则

     • 参与这只能将信件转发给能够直呼其名的熟人，并请他继续转发；如果一个参与者不认识目标收信人，则他不能直接将信寄给他；

     • 参与者需力争让信件尽早达到目的地

     • 第一次：从Kansas的Wichita到哈佛大学神学院某学生的妻子

     • 第二次：从Nebraska的Omaha到Boston的Shanron的股票经纪人Jeffrey Travers

   • 结果

     • 平均中间人数：5

2. 小世界现象

   • 小世界问题

     在Milgram的研究之前，人们感觉世界很小，却没有证据

     • MIT的师生试图证明这一点，不过没有结果

     • 来自Harvard的Milgram用信件进行传递，得到了一个平均数

   • 小世界现象

     —— Milgram的研究证明

     • 世界是小的（六度分隔）；社会网络中包含丰富的短路径

     • “自动寻找”短路径；“有意识的转发”能“自动地“找到这些短路径

   • 启发

     为什么社会网络具有这样的性质？它们源于社会网络的哪些基本原理？

     能否依据社会网络的某些原理，构建出反映这种性质的网络模型？

3. 总结

   一项试图证明“世界是小的”简单研究，提示了或许在人际关系之间，的确存在着某种数学结构

小世界现象的普遍性

后续研究

• 不少重复研究，包括Milgram（1970）自己

• 扩展

  • 运用书信所做的研究具有重复性，电子邮件呢？

  • Dodds, Muhamad and Watts (2003)

    • 60,000个电子邮件用户

    • 通过给熟人转发电子邮件的方式，将邮件送达13个国家的18位收件人

  • 发现

    • 通过认识的人，不一定有多熟悉

    • 中间路径：5-7步

网页之间的“社交”

• 全球互联网超过几百亿的网页，比人口总数多

• 问题

  —— 网页之间，又怎样的关系，也有“小世界”现象吗？

• Albert, Jeong, Barabási(1999); Barabási(2013)

  ——没有关系的两个网页之间的直径为18.59次点击

总结

• 通过熟人送文件（书信）在不断地检验小世界现象的存在

• 即使加上了“种族”的因素，小世界现象依然存在

• 在电子邮件时代，通过熟人转发电子邮件，依然有小世界

• 即使在网页之间的“社交”，也有短路径

关于小世界的 Watts-Strogatz 模型

人类社会的小世界现象

• 社会网络中两节点间包含丰富的短路径

  —— 任意两节点间存在短路径的概率很高

• 短视搜索能够有效地找到这些短路径

  —— 短视搜索：在达到目标节点过程中，每一步只能看到邻居节点

对于“十分稀疏”的社会网络来说，这并不是必然

从现象到问题

问题

• 为什么社会网络具有这样的性质？它们源于社会网络的那些性质？

  • 可以证明，完全随机的网络没有这样的性质

• 换句话说，能否依据社会网络的某些基本原理来证明这种性质的必然性呢？

形成社会网络的两种力量

• 同质性

  • 共同朋友，邻里关系，同学，同事，共同兴趣

  • 对应社会网络中大量的“三角形”（圈子）

• 弱联系

  • 偶然的原因，认识的“远程”朋友

  • 对其所在的圈子并不一定熟悉

能否找到一种形式化网络，既能够体现这两种力量的作用，也便于我们分析其中是否具有小世界现象？

Watts-Strogatz 模型

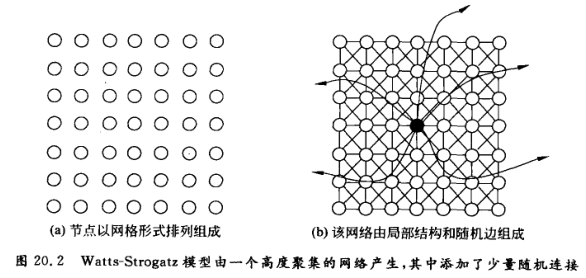
定义一种图（网络），体现上述因素

• 有许多“三角形”和少数随机的“远程边”

  

  • 每两点之间有一个“网格距离”

  • 大量节点拍不成均匀的网格状

  • 连接近邻：确定性，连接远程：随机性

  • 模型中节点间有两个距离的概念：网格距离和网络距离

• 体现了同质连接和弱关系连接的概念，于是可以看成是现实社会网络的一个合理近似

• 可以证明：在这样的网络中，任意两节点之间存在短路径的概率很高

• 也可以证明，Watts-Strogatz模型不能很好滴体现第二个要求

  短视搜索路径太长，尽管短路径存在

总结

• 对于重要的社会现象，如果可以使用一个数学模型来解释，尽管这个模型概括不了现象的所有细节，也是值得追求的

• Watts-Strogatz模型，抽象地表达了社会网络成因的基本特征，从理论上说明了小世界现象（一个方面）的必然性

关于小世界的Watts-Strogatz-Kleinberg 模型

Watts-Strogatz模型的意义与局限性

• 证明了模型网络中任意两个节点之间存在短路径的概率很高，即“小世界”

• 但不能解释Milgram等人实验反映出的小世界现象的另一个层面：在短视搜索情况下能找到短路径

  • 在模型上执行短视搜索，常常导致较长路径

短视搜索（分散搜索）

有目标；每一步只有局部知识；与目标进行对比

• 相对于我们已经熟悉的“广度优先索索”（无目标），这是一种有目标的基于局部信息的搜索，具有如下特点：

  • 每个节点都有一个特征，任何两个节点间的特征可以谈差别（距离） → 不同于图论中定义的距离

  • 每个节点都知道目标节点的特征，也知道自己和自己邻居节点的特征

  • 搜索过程中可以看做是信息传递的过程，节点将信息传递给离目标节点距离较近（差别较小）的邻居节点

• 示例

  

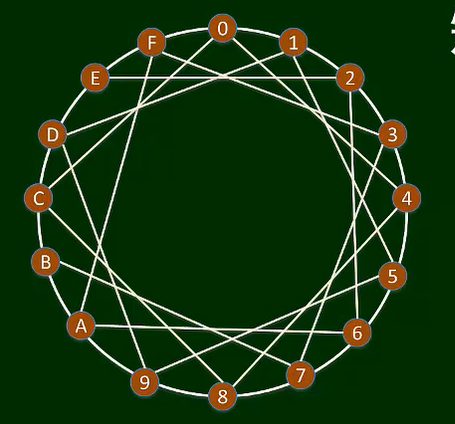
  • 节点：0, 1, …, 9, A, …, F

  • 特征距离（差别）：由环上相对位置定义，例如节点0和A的距离为6

  • 从0开始，以A为目标的短视搜索：0-C-B-A

  • 而不是 0-F-A

  短视搜索没走“最短路径”！

一种一般的认识论方法

• 经常，在事物的宏观格局中存在某种性质，但若缺乏宏观视野，仅凭基于微观视野的追求，不一定能够发现那种特质

• 但如果事物的结构存在某种特征，使我们能够证明，基于微观视野的追求，就能揭示宏观性质，则是十分美妙的事情。

通过局部，了解全局；通过微观，理解宏观

在小世界问题上我们面对：

• 在人类社会网络上的大量实验结果表明：短视搜索是有效的，这说明现实社会网络结构支持这种做法

• 在WS社会网络模型上的理论分析表明，短视搜索效果不好，这说明该模型没能抓住现实网络的某个重要特点

因此，我们需要一种社会网络模型

• 既反映节点对之间短路径的存在性，也支持这种信件转发方式下短路径的可实现性

网络中需要什么样的结构特征来体现这样的要求呢？

• 两个节点无论相距多远，都要有机会很快接近

• 两个节点的距离越近，存在直接连接的机会越大

Watts-Strogatz-Kleinberg模型

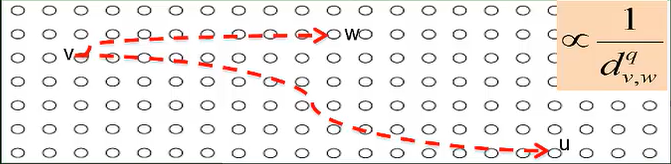
• 在WS模型基础上，让两个节点之间存在随机边的概率与它们网格距离的某个幂次（q）成反比

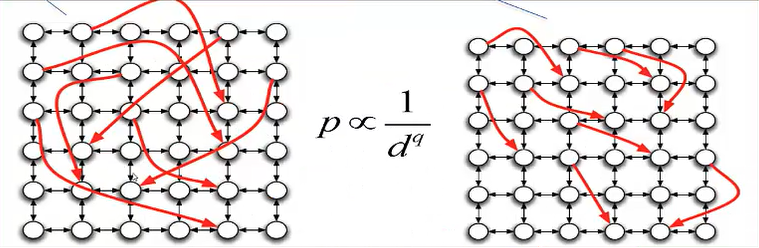
• q值较小，随机边倾向于较远；q值较大，随机边倾向于较近

• Watts-Strogatz模型对应于 $q = 0$ 的情况

改模型的最佳工作参数（q）

• 理论结果：当 $q=2$ 时 ，分散搜索达到最佳效果

• 仿真实验：由几亿个节点组成的网络中，考察不同的 q 值在分散搜索中的效果

  

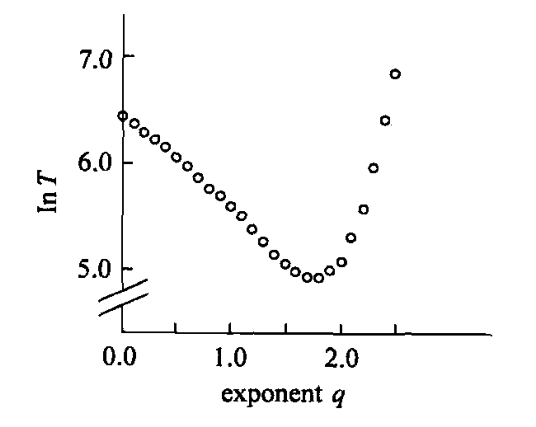
总结

• 发现WS模型不能反映现实社会网络的一个重要特征，促成了WSK模型

• WSK模型通过适当控制WS模型中的随机性，与试验结果更加吻合

• 改模型出现了一个优化参数（q），当取特定值时效果最好，这个参数在现实社会网络中如何体现的呢？

WSK模型中优化参数的大数据验证

Milgram的实验表明，现实社会网络中，分散搜索的路径很短。于是很值得好奇：难道人们成为朋友的概率真的岁空间距离递减，并且递减强度幂次 q 真的等于 2 吗？

利用在线社会网络进行验证

• 真实大规模在线社会网络是否体现了这个（WSK）网络模型的优化性质？

  两人成为朋友的概率与其空间距离的平方成反比

• 如果是，则说明随即形成的社会网络可能具有某种本质参数！

• 但，在线社会网络的节点如何谈空间距离？

来自LiveJournal的实验数据

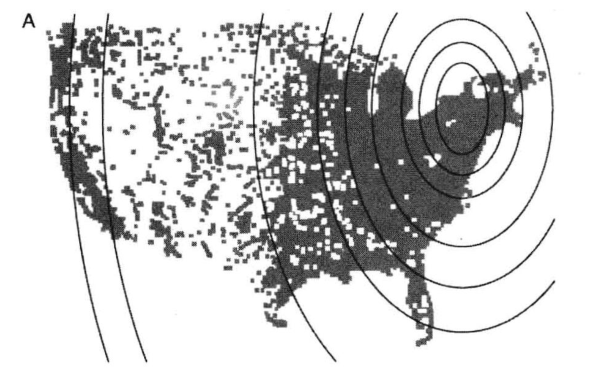
• 50万用户，含邮政编码

• 分布不均匀，不符合模型的假设，需要做一些适配性工作

社会网络中结合地理距离的节点相对排名

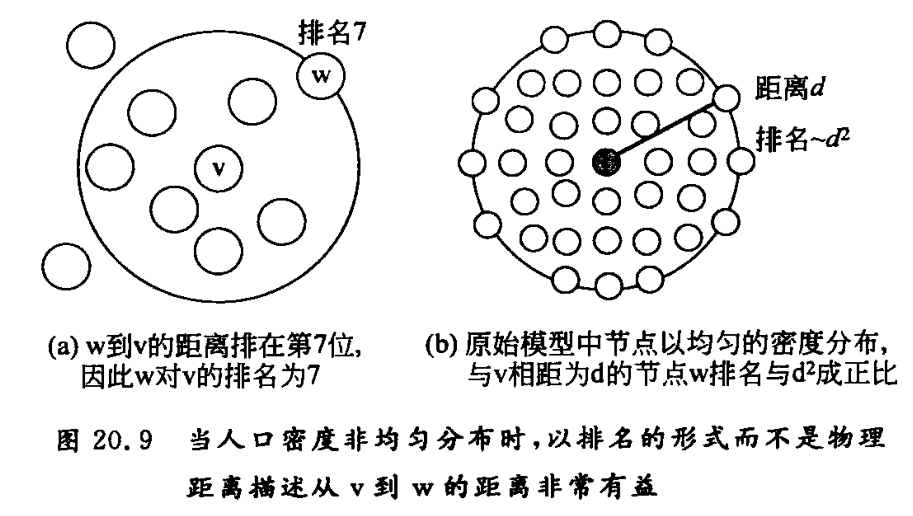
• 可以看成是节点在地理距离上均匀分布时区域范围概念的一种推广，“排名”与“距离”有对应关系

• 这就是我们能一般性地处理节点在地理上分布不均匀的问题

要验证的是：

• 在均匀地理分布情形，一个节点在任意距离上的朋友数量在同等距离节点总数中的占比随距离平方递减 $\frac{1}{d^2}$

此时等价于看

• 一个节点在任一排名上的朋友（即有连接）数量在同等排名节点总数的占比随排名递减 $\frac{1}{r}$

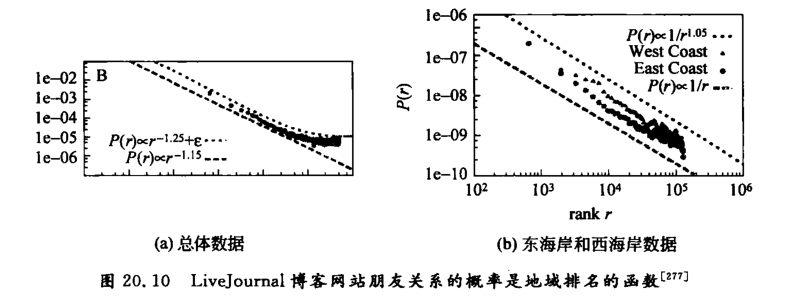
这意味着，大量微观社交关系的建立总体上呈现出一种最优化特征，或者说大量人群的随机社会活动相当于一台计算机，完成了一种优化计算（实现了最优参数）—— 这可以看成是社会计算的一个实例，也是体现社会系统中微观与宏观关系的实例。

总结

• 前面的内容，讨论了人们围绕小世界现象所展开的一系列研究思路

• 看到了“实验 → 理论 → 完善 → 实验”研究范式的体现

  （小世界）现象 → 抽象模型（解释现象） → 完善模型 （更好地解释） → 数据验证（得到对现实更深入的认识）

• 也看到了大数据分析在推进这类研究中的作用

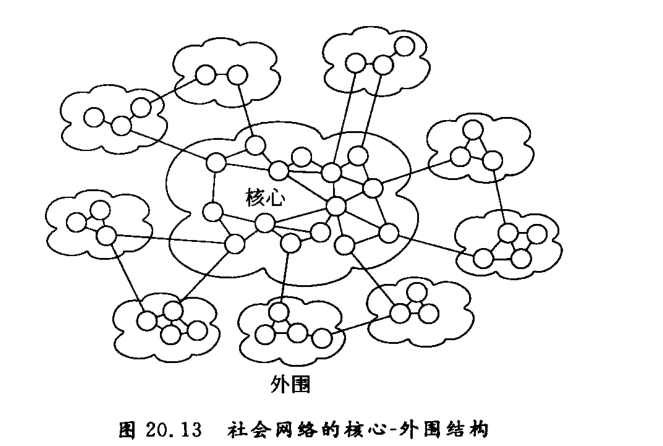
核心—外围结构：一种社会网络观

核心-边缘结构模型

• Borgatti 和 Everett (1999) 观察到，在社会网络中

  • 地位较高的人，被连接在一个密集连接的核心

  • 地位较低的人，都分散在网络外围

• 核心 - 边缘结构

  • 不仅是在理论上

  • 现实社会中，普遍存在

• 

理论与现实

• 理论上

  处在网络结构中的节点，不同的节点如果有相同的聚集系数，其被连接到的概率是一样的

• 现实中

  • Milgram(1967)的第一次试验就已经暗示：寻找地位较低得人（神学院学生的妻子）会更加困难

  • 人们观察到，“媒体寻人”较之个体寻人有更高的成功率

  • 回想“结构洞”，处于结构洞位置上的人，其被找到的概率，远远大于一般节点上的人

社会意义

• 如果处于更高的社会地位，且在结构洞的位置上呢？故

  • 网络结构本身是重要的，尤其在可计算性上

  • 同样重要的是，网络结构的社会属性

  • 具有相同网络结构，却有着不同的社会属性的网络，在显示社会中，具有布偶听的“可连通性”（社会含义）

  • 社会地位较高的人，具有更多的“关系资源”，更好的连通性

总结

• 网络结构会因为节点上的人的社会属性不同，而有不同

• 社会地位较高的人，倾向于有更多的、更广的关系（连接）

• 即，社会属性是影响网络结构及其连通性的重要因素