2020-03-02发表2020-03-02更新社会计算16 分钟读完 (大约2378个字)

Social computing 1 —— 网络与市场中的计算思维

1. 网络与图论

图是网络结构信息的抽象，表达的是网络中各种事物之间的关系。

一个简单图是集合 $X = (V, E)$ ，其中 $V$ 是定点， $E$ 是边。一条边连接的两个顶点称为它的两端点。其实我们可以把一条边看作 $V$ 的子集，其中有两个顶点。一个简单图就是一个无向图，它不会有圈或者重边。若 $u \not = v$ 是两个顶点， ${u, v}$ 是一条边，那么两顶点相邻，记为 ${u, v}$ 。
同一个图，可能有多种不同的画法。也就是说，同一个图可能呈现出不同的图像形式。

同构图 在图论中，假设 $G=(V, E)$ 和 $G1 = (V1, E1)$ ，如果存在一个双射 $m: V → V1$ ，使得对所有的 $x, y ∈ V$ 均有 $xy ∈ E$ 等价于 $m(x)m(y)∈ E1$ ，则称 $G$ 和 $G1$ 是同构的，这样的一个映射 $m$ 称之为同构，如果 $G = G1$ ，则称他们为一个自同构。
路径（walk）

一个长度为 $k$ 的路径是一个费控的顶点和边的交错序列 $v_0e_0v_1e_1...e_{k-1}v_k$ ，使得对于所有 $i < k$ 均有 $e_i = v_iv_{i+1}$ 。特别的，当 $v_0 = v_k$ 时，称这个路径为闭的（close）；当路径中的顶点互不相同，得到 $G$ 的一条路。
连通图
- 在无向图 $G$ 中，若从顶点 $v_i$ 到顶点 $v_j$ 有路径（当然从 $v_j$ 到 $v_i$ 也一定有路径），则称 $v_i$ 和 $v_j$ 是连通的。
- 如果G是有向图，那么连接 $v_i$ 和 $v_j$ 的路径中所有的边都必须同向。如果图中任意两点都是连通的，那么图被称作连通图。
连通分量
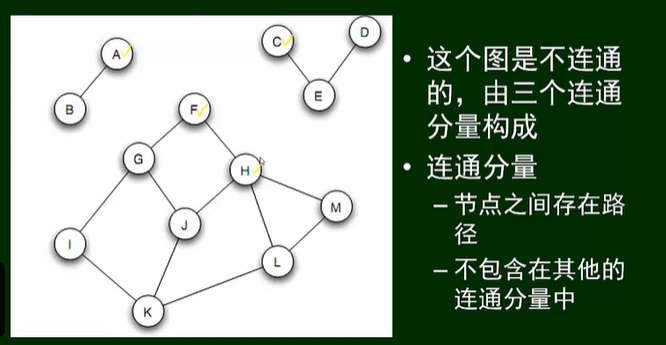
- 无向图G的一个极大连通子图称为G的一个连通分量（或连通分支）。连通图只有一个连通分量，即其自身；非连通的无向图有多个连通分量。
- 有向图G= (V,E)中，若对于V中任意两个不同的顶点 x和y，都存在从x到y以及从y到x的路径，则称G是强连通图（Strongly Connected Graph）。相应地有强连通分量的概念。强连通图只有一个强连通分量，即是其自身；非强连通的有向图有多个强连通分量。
二部图
- 二分图的顶点可以分成两个互斥的独立集U和 V的图，使得所有边都是连结一个 U 中的点和一个 V 中的点。顶点集 U、V 被称为是图的两个部分。等价的，二分图可以被定义成图中所有的环都有偶数个顶点。
- 许多社会现象或状态的结构，都呈现出二部图的形式
- 是否有长度为奇数的圈，是判断一个图是否是二部图的充分必要条件。
- 长度优先搜索（遍历），是考察一个图是否存在长度为奇数的圈的有效方法。
  
  从任何节点开始，在广度优先搜索（遍历）过程中，一旦发现同一层节点之间有边，则图中一定存在长度为奇数的圈，则该图不是二部图。
三元闭包
- 不仅考虑一个时刻（“快照”）上的状态
- 还要研究随时间发生的变化（内部原因 vs 外部原因）
社会网络眼花的基本结构性原因（Anatole Rapoport, 1953）
- 三元闭包(triadic closure) 在一个社交圈内，若两个人有一个共同的朋友，则这两人在未来成为朋友的可能性会提高。
  - 机会（opportunity）
  - 信任（trust）
  - 动机（incentive）
- 林南
  - 一个特定的网络可以自然地形成
  - 也可以有对一个特定的共同关注的焦点或关注一种资源利益的社会性建构
聚集系数

刻画某个节点的重要性
- 结构洞
- 聚集系数，就是在三元闭包中，对一个节点属性的测度，表示“凝聚力”的大小
  
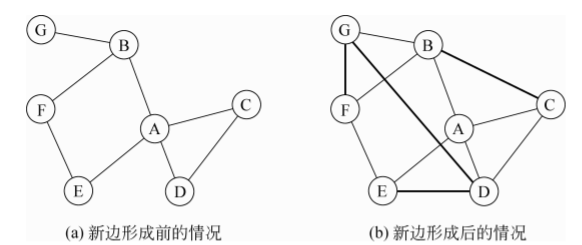
  节点A的聚集系数 = 与A相邻的任意两个朋友之间也是朋友的概率 = 与A相邻的朋友对的个数/总数
  
  在上图a中，节点A的聚集系数 $1/6$ （因为与A相邻的6个节点对B-C、B-D、B-E、C-D、C-E 和 D-E 中，仅有一个边 C-D ）。
三元闭包的大数据验证
- 电子邮件网络~~社会网络
  
  可能性：共同朋友 -> 成为朋友的概率
  
  数据验证要求：
  - 网络规模足够大
  - 数据跨度时间足够长
- 关键：
  - 将社会科学原理的定性描述，转化为便于定量分析的表述，形成数据指标（与共同朋友书对应的概率）。
  - 选择合适的数据，以及从原始数据中提炼出指标数据的方法。
强关系与弱关系

Granovetter(1973)提出了刻画边的属性的一种测度：强 – 弱。被动参与三元闭包原理实际上暗含了一个随时间推移的可能。
- 有的人会被动加入某些网络
- Huberman et al. (2009) 对Twitter的研究表明，即使所有朋友的总数超过500，实际联系的总数也在10-20人之间；被动联系人的数量也不超过50人。
嵌入性（Embedness）
- Karl Polanyi (1944) 《大转变》行动嵌入制度。
- Granovetter (1985) 在与经济学家的论战中，提出了经济行为与社会结构之间的关系问题，拓展了嵌入性概念，指出，经济行为是嵌入在社会结构之中的，是社会行为的一种。
网络分析，恰恰是Granovetter从他老师Harrison White (1967) 那里得到的衣钵。

嵌入性：边的属性
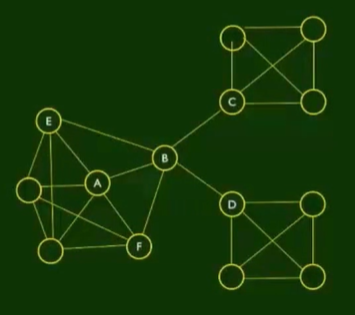
- 嵌入性 = 一条边两端共同的邻里数
- 看 A - B 边，有共同的邻里 E 和 F，则 A-B 边的嵌入性为 2
- 嵌入性越强的边，相互之间的信任就越强；嵌入性越强的边，社会资源也就越多
- 嵌入性与社会资本是两个不同分析框架的概念。
结构洞（结构位置整体）
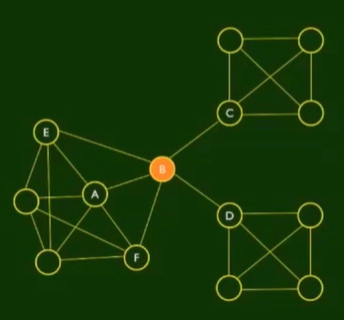
- 一个节点，移除该节点就会使网络变成多个连通分量的节点
- 节点B，移除它，就会变成3个连通分量
- 结构洞意义
  - 了解三方面的信息
  - 处于捷径的一端，对其 “长处” 有放大影响
  - 对于其相邻的节点甚至具有“权力”
  - 冗余（凝聚力冗余和结构等位冗余）越小的结构洞，社会资本就越多（Burt的结构洞）
强三元闭包

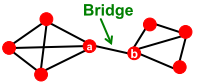
桥(Bridge)：如果一个图中，已知A和B相连，若去掉连接A和B的边导致A和B分属不同的连通分量，则该边称为桥。桥为A、B间唯一路径。

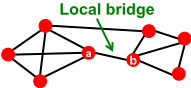
捷径(Local bridge)：若边A-B的端点A和B没有共同朋友，则称边A-B为捷径；删除A-B边将把A-B距离增加至2以上。

强联系：对应朋友(Friend)关系。弱联系：对应熟人(Acquaintance)关系；通过捷径找到工作；亲密团体内信息多数自己已经知道。

两人关系的强度与是否有共同朋友直接相关，捷径意味着没有共同朋友，强度为弱，共同朋友数越多，关系的强度越高。

强三元闭包原理：如果 A 和 B、C之间的关系分别为强关系；则 B 和 C 之间形成边的可能性应该很高。
- 若A有两个强关系邻居B和C，但B和C之间没有任何关系（s或w），则称节点A违背了强三元闭包远离
- 如果节点A没有违背强三元闭包原理，则称节点A符合强三元闭包原理
断言：若节点A符合强三元闭包，且至少有两个强关系邻居，则与A相连的任何捷径必定意味着是弱关系。

强三元闭包原理的精神：没有共同朋友 -> 捷径 -> 弱关系

定量化表述：共同朋友越多，关系强度越
- 也就是社交网络中，我们预计看到人们关系的强度与共同朋友数正相关